關鍵要點:
- 在 Excel 中計算加權平均對於準確的財務分析、學業評分和存貨估值至關重要,但傳統公式如
SUMPRODUCT需要專業的 Excel 知識。 - Excelmatic 無需記憶複雜公式,讓您可以使用簡單的語言指令計算加權平均。
- 與手動公式方法相比,Excelmatic 能即時處理複雜的多條件計算,減少錯誤並節省寶貴時間。
- 對於市場行銷、銷售和營運領域的商業專業人士而言,採用像 Excelmatic 這樣的 AI 工具意味著可以專注於數據洞察,而非技術實現。
加權平均在數據分析中無處不在,從計算 GPA 到確定投資組合回報。與平等對待所有數據點的簡單平均不同,加權平均認識到某些值比其他值更具影響力。這使得它們在處理重要性或頻率不同的數據時非常有用。
什麼是加權平均?
加權平均根據預先確定的權重,為各個數據點分配不同級別的重要性。簡單平均平等對待所有值,而加權平均則在計算最終結果之前,將每個值乘以其對應的權重。
關鍵在於:權重直接控制每個數據點對最終平均值的影響程度。權重較高的數據點會將結果拉近其值,而權重較低的點影響較小。這讓您對計算有更多的控制,通常能產生更有意義的結果。
加權平均與簡單平均有一個重要區別:它們考慮了每個數據點的相對重要性,而不是假設所有點都同等重要。
理解加權平均公式
現在我們已經確定了加權平均是什麼以及為什麼重要,讓我們深入探討使其運作的數學基礎。
數學定義與核心原則
加權平均公式將每個數據點與其對應的權重結合:
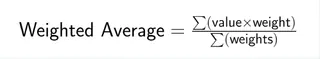
其中 Σ 表示所有項的總和。每個值乘以其權重,然後將所有這些乘積相加,再除以所有權重的總和。
在大多數實際情境中(機率、頻率和份額),權重為非負數,並且通常歸一化為總和為 1(或總計數)。在專業方法中,可能會出現負權重,但可能產生違反直覺的結果,應謹慎使用。始終確保權重總和大於零,以避免除以零的錯誤。
此公式確保權重較高的值對最終結果有按比例更大的影響。例如,如果一個數據點的權重為 10,另一個的權重為 1,則第一個點對最終平均值的貢獻是十倍。
歸一化與特殊情況
歸一化意味著縮放權重使其總和為 1,使每個權重可以直接解釋為百分比貢獻。當 $(sum_i w_i = 1)$ 時,加權平均簡化為 $(sum_i w_i x_i)$。在機率情境中,這些權重就是機率,而加權平均就是期望值。
這種歸一化方法在機率情境中特別有用,其中權重代表必須總和為 1 的機率。在這些情況下,加權平均就成為該分佈的期望值。
為何及何時使用加權平均
有了數學基礎,您可能想知道何時加權平均比簡單平均是更好的選擇。答案在於識別您的數據何時自然具有不同級別的重要性。
當您的數據點自然具有不同級別的重要性或頻率時,加權平均就變得至關重要。當數據點代表不同的樣本大小、時間段或可靠性級別時,您會發現加權平均比簡單平均效果更好。例如,在計算不同班級規模的平均考試分數時,較大的班級應該比較小的班級對整體平均有更大的影響。
加權平均在財務計算(投資組合回報)、學業評分(不同作業權重)、調查分析(人口統計調整)和庫存管理(不同採購數量的成本平均)中特別有價值。
加權平均的常見挑戰
雖然加權平均是強大的工具,但它們也伴隨著一系列潛在的陷阱,您需要小心應對。
權重選擇
最關鍵的挑戰在於選擇適當的權重,這需要領域專業知識並仔細考慮每個數據點所代表的含義。糟糕的權重選擇可能會嚴重扭曲結果,導致誤導性的結論。
例如,如果您正在計算客戶滿意度分數,卻錯誤地將較高的權重分配給不太可靠的數據來源,您的最終平均值將無法準確反映真實的客戶情緒。始終確保您的權重反映了每個數據點的實際重要性或可靠性。
計算陷阱
除了權重選擇之外,常見的計算錯誤包括使用零權重(這會移除數據點)、負權重(可能產生違反直覺的結果)以及在必要時忘記歸一化權重。當所有權重為零時會發生除以零的錯誤。
始終仔細檢查您的權重分配,並確保適當的歸一化,尤其是在處理應總和為 100% 的基於百分比的權重時。
如何計算加權平均:Excel、AI 和 Python
介紹了理論和潛在挑戰後,讓我們轉向實務面。計算加權平均可以通過多種方式完成,從傳統公式到現代AI 驅動工具。
方法 1:傳統 Excel 方法(使用公式)
Excel 使用 SUMPRODUCT() 和 SUM() 函數使加權平均計算變得簡單明瞭。SUMPRODUCT 將給定陣列中的對應組件相乘,並返回這些乘積的總和。
公式結構為:
=SUMPRODUCT(values, weights)/SUM(weights)
例如,如果您的值在儲存格 A2:A6 中,其對應的權重在 B2:B6 中,則公式為:
=SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6)
這種方法可靠,但需要您知道正確的函數並確保儲存格範圍準確。對於大型或動態數據集,管理這些公式可能會變得繁瑣。
方法 2:現代 AI 方法(使用 Excelmatic)
更快、更直觀的方法是使用像 Excelmatic 這樣的 AI Excel 助手。無需編寫公式,您只需用簡單的語言陳述您的請求。Excelmatic 會處理其餘部分,從解釋您的請求到執行計算。
運作方式如下:
- 上傳包含值和權重的 Excel 檔案。
- 用簡單語言提出您的問題。
對於相同的例子,您只需詢問:
使用 B 欄的權重計算 A 欄值的加權平均。
Excelmatic 會立即處理您的數據並提供答案,無需記憶公式或擔心儲存格引用。
比較:傳統公式 vs. AI 助手
| 特性 | 傳統 Excel (SUMPRODUCT) | AI 驅動的 Excelmatic |
|---|---|---|
| 所需努力 | 需要了解 SUMPRODUCT 和 SUM 函數及正確語法。 |
只需用簡單語言提問。無需公式。 |
| 速度 | 對有經驗的用戶來說很快,但容易出現拼寫錯誤和範圍錯誤。 | 即時。AI 處理所有後端計算。 |
| 靈活性 | 僵化。如果數據範圍改變,必須手動更新公式。 | 高度靈活。AI 理解上下文並適應新問題。 |
| 學習曲線 | 中等。您需要學習並記住特定的 Excel 函數。 | 幾乎為零。如果您能提問,您就能使用它。 |
使用像 Excelmatic 這樣的 AI 工具不僅簡化了流程,還減少了人為錯誤的機會,使您的分析更快、更準確。
方法 3:如何在 Python 中計算加權平均
對於使用 Python 的人,NumPy 庫提供了一個優雅的解決方案,儘管您也可以手動計算加權平均:
import numpy as np
# 定義值和權重
values = [85, 92, 78, 95]
weights = [0.2, 0.3, 0.25, 0.25]
# 計算加權平均
weighted_avg = np.average(values, weights=weights)
print(f"加權平均: {weighted_avg:.2f}")
# 替代手動計算
manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)
print(f"手動計算: {manual_calc:.2f}")
加權平均公式在實際、特定領域的應用
現在您知道如何計算加權平均了,讓我們探討它們如何解決不同領域的實際問題。這些例子將幫助您識別加權平均可以改善您自己分析的情況。
教育評分系統
學術評分系統通常使用加權平均來平衡不同類型的評估。一門典型的課程可能將考試權重設為 60%,作業為 25%,參與度為 15%。
如果一名學生考試得分 88,作業得分 95,參與度得分 92,其最終成績為:(88×0.6) + (95×0.25) + (92×0.15) = 90.35。這種方法確保更重要的評估對最終成績有更大的影響。
財務存貨估值
在商業應用中,公司通常使用加權平均成本法在一個期間內以不同價格購買商品時對存貨進行估值。與簡單的算術平均不同,WAC 結合了採購數量,這平滑了價格波動,並為財務報告提供了穩定的成本基礎。
例如,如果一家公司以 10 美元購買 100 單位,以 12 美元購買 300 單位,則加權平均成本為 11.50 美元,而不是簡單平均所建議的 11.00 美元。
財務分析
在金融領域,加權平均的應用遠不止於存貨。投資組合管理依賴它們來計算預期回報和風險,每個資產的權重基於其在總投資組合價值中的比例。這確保了較大的持倉比較小的持倉有更大的影響力。
同樣地,加權平均資本成本也應用相同的原則:它通過按債務和股權在資本結構中所佔比例加權其成本,來代表公司的平均融資成本。WACC 是估值模型和投資決策的關鍵輸入,因為它作為公司產生回報的門檻率。
統計調查
在研究領域,調查分析使用加權平均來調整人口統計不平衡並確保具有代表性的結果。如果您的調查對某些年齡組抽樣不足,您可以對回應進行加權以匹配實際的人口分佈。
這種調整有助於消除抽樣偏差,並產生關於您所研究的更廣泛人群的更準確洞察。
存貨會計
回到實際的商業應用,存貨會計中的移動平均法使用加權平均來確定銷貨成本。每次新採購都會根據剩餘存貨和新增加的部分更新每單位平均成本。
這種方法平滑了價格波動,並為財務報告提供了穩定的成本估算,使得更容易追蹤隨時間變化的盈利能力趨勢。
面積加權建築輸入及其他專業情境
除了這些常見應用之外,工程應用通常使用面積加權平均進行建築能源計算,其中不同區域根據其大小對整體建築性能做出貢獻。
類似的概念出現在地理資訊系統中用於空間分析,以及製造業中用於不同生產區域的品質控制。
與其他平均值的比較分析
考慮到所有這些應用,您可能想知道如何在加權平均和其他平均方法之間進行選擇。理解這些區別將幫助您為特定情況選擇正確的方法。
算術平均 vs. 加權平均
算術平均假設所有數據點同等重要且具有代表性。加權平均明確考慮了數據點之間在重要性、可靠性或頻率上的差異。
當您的數據自然具有不同級別的重要性,或者當您需要調整抽樣不平衡時,請選擇加權平均。當所有數據點確實值得同等考慮時,請使用簡單的算術平均。
幾何平均
幾何平均最適合乘法數據,如增長率或比率,您希望找到隨時間變化的平均變化率。然而,幾何平均不能自然地容納加權。
雖然您可以使用對數創建加權幾何平均,但這種方法在數學上很複雜,並且對於大多數應用來說不如加權算術平均直觀。
加權平均的優點和缺點
在深入探討更高級的主題之前,值得退一步考慮使用加權平均所涉及的更廣泛的權衡。
加權平均的優點
當數據點自然在重要性或可靠性上有所不同時,加權平均提供了更高的準確性。它們提供了根據領域知識調整計算的靈活性,並且可以更好地代表現實世界場景,其中並非所有觀察都是平等的。
這種方法在需要人口統計調整、投資組合分析或任何樣本大小或測量置信度在數據點之間變化的情境中表現出色。
加權平均的缺點
主要限制在於權重選擇的主觀性,如果做得不好,可能會引入偏差。加權平均對具有高權重的異常值也更敏感,並且如果權重分配不正確,容易出錯。
此外,與簡單平均相比,它們需要更多的計算工作和領域專業知識,這使得它們在平等加權適用的情況下顯得過於複雜。
更高級和理論上的延伸
對於有興趣超越基本應用的讀者,加權平均可以延伸到更複雜的數學領域,開啟了額外的分析可能性。
連續加權平均
加權平均可以使用積分擴展到連續函數。不是離散的權重和值,而是對連續的權重和值函數進行積分:
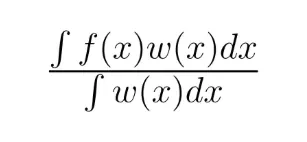
這種方法出現在物理學中用於計算質心,以及在機率論中用於連續分佈。
機率中的期望值
在此數學基礎上,在機率論中,期望值代表所有可能結果的加權平均,其中權重是每個結果發生的機率。
期望值有助於預測不確定情況下的長期結果,從賭場遊戲到投資回報,使它們成為風險評估和決策制定的重要工具。
結論
當您的觀察在重要性、頻率或可靠性上自然不同時,加權平均提供了一種更細緻、更準確的數據分析方法。從學業評分到投資組合管理,它們通過適當考慮不同數據點的相對重要性來增強決策制定。
當您開始將加權平均納入您的分析時,請記住,該技術的力量來自於其反映現實世界複雜性的能力。無論您是使用 SUMPRODUCT 的公式高手,還是利用 AI 助手的速度,目標都是一樣的:通過給予最重要的信息適當的影響力,做出更明智的決策。
準備好簡化您的加權平均計算,專注於洞察而非公式嗎?立即免費試用 Excelmatic,體驗 AI 驅動的數據分析如何改變您的工作流程。
加權平均公式常見問題解答
如何確定加權平均的權重?
權重選擇取決於您的具體情境並需要領域專業知識。常見方法包括使用樣本大小(較大的樣本獲得較高的權重)、可靠性分數(更準確的測量獲得較高的權重)、時間段(較新的數據獲得較高的權重)或業務重要性(關鍵指標獲得較高的權重)。始終確保權重反映每個數據點的實際重要性。
能否提供金融領域加權平均的實際例子?
金融應用包括投資組合回報(每支股票按其佔總投資的百分比加權)、加權平均資本成本(債務和股權成本按其比例加權)、信用評分(不同因素按重要性加權)和存貨估值(採購成本按數量加權)。這些應用認識到不同組件對最終結果的貢獻是不相等的。
加權平均和簡單平均有什麼區別?
簡單平均平等對待所有數據點,而加權平均為每個點分配不同級別的重要性。當所有觀察都同樣有效且具有代表性時,簡單平均效果很好。當數據點在樣本大小、可靠性、重要性或頻率上有所不同時,加權平均更優越。選擇取決於平等對待所有數據點是否適合您的特定情況。
當權重總和不為 1 時,如何計算加權平均?
當權重總和不為 1 時,使用標準公式:將(值 × 權重)的總和除以所有權重的總和。例如,值為 [80, 90, 95],權重為 [2, 3, 5],計算:(80×2 + 90×3 + 95×5) ÷ (2+3+5) = 90.5。該公式會自動歸一化權重,因此您無需手動調整它們使其總和為 1。
為什麼在某些情況下加權平均比簡單平均更受青睞?
當數據點自然具有不同級別的重要性、可靠性或代表性時,加權平均更受青睞。例如,在計算平均客戶評分時,來自驗證購買者的評論可能比匿名評論更值得加權。同樣地,在調查研究中,回應需要加權以匹配人口統計數據。每當平等對待所有數據點會產生誤導性結果時,請使用加權平均。
加權平均可以與非數值權重一起使用嗎?
不可以,權重必須是代表每個數據點相對重要性或頻率的數值。但是,您可以將分類重要性級別(如「高」、「中」、「低」)轉換為數值權重(如 3, 2, 1)。關鍵在於確保您的數值權重準確反映您想分配給每個數據








