Principais Conclusões:
- Calcular médias ponderadas no Excel é essencial para análises financeiras precisas, avaliações acadêmicas e valoração de estoque, mas fórmulas tradicionais como
SUMPRODUCTexigem conhecimento técnico do Excel. - O Excelmatic elimina a necessidade de memorizar fórmulas complexas, permitindo que você calcule médias ponderadas usando comandos simples em linguagem natural.
- Comparado aos métodos manuais com fórmulas, o Excelmatic lida com cálculos complexos de múltiplos critérios instantaneamente, reduzindo erros e economizando tempo valioso.
- Para profissionais de negócios em marketing, vendas e operações, adotar ferramentas de IA como o Excelmatic significa focar em insights de dados em vez de implementação técnica.
As médias ponderadas aparecem em todos os lugares na análise de dados, desde o cálculo da sua média de notas (GPA) até a determinação dos retornos de uma carteira de investimentos. Diferente das médias simples, que tratam todos os pontos de dados igualmente, as médias ponderadas reconhecem que alguns valores merecem mais influência que outros. Isso as torna incrivelmente úteis quando você está lidando com dados de importância ou frequência variadas.
O Que É uma Média Ponderada?
Uma média ponderada atribui diferentes níveis de importância a pontos de dados individuais com base em pesos predeterminados. Enquanto uma média simples trata todos os valores igualmente, uma média ponderada multiplica cada valor pelo seu peso correspondente antes de calcular o resultado final.
Aqui está o insight principal: os pesos controlam diretamente o quanto cada ponto de dados influencia a média final. Um ponto de dados com um peso maior puxa o resultado para mais perto do seu valor, enquanto pontos com peso menor têm menos impacto. Isso dá a você muito mais controle sobre seus cálculos e frequentemente produz resultados mais significativos.
As médias ponderadas diferem das médias simples de uma maneira importante: elas levam em conta a significância relativa de cada ponto de dados, em vez de assumir que todos os pontos são igualmente importantes.
Entendendo a Fórmula da Média Ponderada
Agora que estabelecemos o que são médias ponderadas e por que são importantes, vamos mergulhar na base matemática que as faz funcionar.
Definição matemática e princípios fundamentais
A fórmula da média ponderada combina cada ponto de dados com seu peso correspondente:
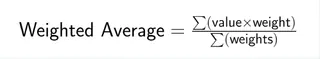
Onde Σ representa a soma de todos os termos. Cada valor é multiplicado pelo seu peso, depois você soma todos esses produtos e divide pelo total de todos os pesos.
Na maioria dos contextos práticos (probabilidades, frequências e participações), os pesos são não negativos e frequentemente normalizados para somar 1 (ou para a contagem total). Em métodos especializados, pesos negativos podem aparecer, mas podem gerar resultados contra-intuitivos e devem ser usados com cuidado. Sempre garanta que a soma dos pesos seja maior que zero para evitar divisão por zero.
Esta fórmula garante que valores com pesos mais altos tenham influência proporcionalmente maior no resultado final. Por exemplo, se um ponto de dados tem um peso de 10 e outro tem um peso de 1, o primeiro ponto contribui dez vezes mais para a média final.
Normalização e casos especiais
Normalização significa escalar os pesos para que eles somem 1, tornando cada peso diretamente interpretável como uma porcentagem de contribuição. Quando $(sum_i w_i = 1)$, a média ponderada se simplifica para $(sum_i w_i x_i)$. Em contextos de probabilidade, esses pesos são probabilidades e a média ponderada é o valor esperado.
Esta abordagem normalizada é especialmente útil em contextos de probabilidade, onde os pesos representam probabilidades que devem somar 1. Nestes casos, a média ponderada se torna o valor esperado da distribuição.
Por Que e Quando Usar Médias Ponderadas
Com a base matemática estabelecida, você pode estar se perguntando quando as médias ponderadas se tornam a escolha melhor do que as médias simples. A resposta está em reconhecer quando seus dados naturalmente têm níveis variados de significância.
As médias ponderadas se tornam essenciais quando seus pontos de dados naturalmente têm diferentes níveis de importância ou frequência. Você descobrirá que as médias ponderadas funcionam melhor do que as médias simples quando os pontos de dados representam tamanhos de amostra diferentes, períodos de tempo diferentes ou níveis de confiabilidade diferentes. Por exemplo, ao calcular a média de notas de testes em diferentes tamanhos de turma, turmas maiores devem influenciar a média geral mais do que turmas menores.
As médias ponderadas são particularmente valiosas em cálculos financeiros (retornos de carteira), avaliação acadêmica (pesos diferentes de tarefas), análise de pesquisas (ajustes demográficos) e gestão de estoque (média de custos entre diferentes quantidades de compra).
Desafios Comuns com Médias Ponderadas
Embora as médias ponderadas sejam ferramentas poderosas, elas vêm com seu próprio conjunto de armadilhas potenciais que você vai querer navegar com cuidado.
Seleção de pesos
O desafio mais crítico está em escolher pesos apropriados, o que requer expertise de domínio e consideração cuidadosa do que cada ponto de dados representa. Uma seleção ruim de pesos pode distorcer os resultados dramaticamente e levar a conclusões enganosas.
Por exemplo, se você está calculando pontuações de satisfação do cliente e acidentalmente atribui pesos mais altos a fontes de dados menos confiáveis, sua média final não refletirá com precisão o verdadeiro sentimento do cliente. Sempre garanta que seus pesos reflitam a importância ou confiabilidade real de cada ponto de dados.
Armadilhas computacionais
Além da seleção de pesos, erros computacionais comuns incluem usar pesos zero (que remove pontos de dados), pesos negativos (que podem produzir resultados contra-intuitivos) e esquecer de normalizar os pesos quando necessário. A divisão por zero ocorre quando todos os pesos são zero.
Sempre verifique novamente suas atribuições de peso e garanta a normalização adequada, especialmente ao trabalhar com pesos baseados em porcentagem que devem somar 100%.
Como Calcular Média Ponderada: Excel, IA e Python
Tendo coberto a teoria e os desafios potenciais, vamos para o lado prático. Calcular uma média ponderada pode ser feito de várias maneiras, desde fórmulas tradicionais até modernas ferramentas com IA.
Método 1: O Método Tradicional do Excel (Usando Fórmulas)
O Excel torna os cálculos de média ponderada diretos usando as funções SUMPRODUCT() e SUM(). SUMPRODUCT multiplica os componentes correspondentes nos arrays fornecidos e retorna a soma desses produtos.
A estrutura da fórmula é:
=SUMPRODUCT(valores, pesos)/SUM(pesos)
Por exemplo, se seus valores estão nas células A2:A6 e seus pesos correspondentes estão em B2:B6, a fórmula seria:
=SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6)
Este método é confiável, mas requer que você conheça as funções corretas e garanta que seus intervalos de células estejam precisos. Para conjuntos de dados grandes ou dinâmicos, gerenciar essas fórmulas pode se tornar complicado.
Método 2: O Método Moderno com IA (Usando Excelmatic)
Uma abordagem mais rápida e intuitiva é usar um Agente de IA para Excel como o Excelmatic. Em vez de escrever fórmulas, você pode simplesmente declarar sua solicitação em linguagem natural. O Excelmatic cuida do resto, desde interpretar sua solicitação até realizar o cálculo.
Veja como funciona:
- Faça upload do seu arquivo Excel contendo os valores e pesos.
- Faça sua pergunta em linguagem natural.
Para o mesmo exemplo, você simplesmente perguntaria:
Calcule a média ponderada dos valores na coluna A usando os pesos na coluna B.
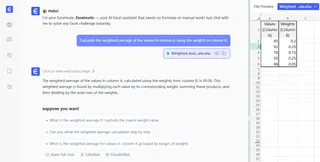
O Excelmatic processa seus dados instantaneamente e fornece a resposta, eliminando a necessidade de lembrar fórmulas ou se preocupar com referências de células.
Comparação: Fórmula Tradicional vs. Agente de IA
| Característica | Excel Tradicional (SUMPRODUCT) | Excelmatic com IA |
|---|---|---|
| Esforço | Requer conhecimento das funções SUMPRODUCT e SUM e da sintaxe correta. |
Basta perguntar em linguagem natural. Nenhuma fórmula necessária. |
| Velocidade | Rápido para usuários experientes, mas propenso a erros de digitação e de intervalo. | Instantâneo. A IA cuida de todos os cálculos de backend. |
| Flexibilidade | Rígida. A fórmula deve ser atualizada manualmente se os intervalos de dados mudarem. | Altamente flexível. A IA entende o contexto e se adapta a novas perguntas. |
| Curva de Aprendizado | Moderada. Você precisa aprender e lembrar funções específicas do Excel. | Praticamente zero. Se você pode fazer uma pergunta, pode usá-lo. |
Usar uma ferramenta de IA como o Excelmatic não apenas simplifica o processo, mas também reduz a chance de erro humano, tornando sua análise mais rápida e precisa.
Método 3: Como Calcular Média Ponderada em Python
Para aqueles que trabalham em Python, a biblioteca NumPy fornece uma solução elegante, embora você também possa calcular médias ponderadas manualmente:
import numpy as np
# Definir valores e pesos
valores = [85, 92, 78, 95]
pesos = [0.2, 0.3, 0.25, 0.25]
# Calcular média ponderada
media_ponderada = np.average(valores, weights=pesos)
print(f"Média ponderada: {media_ponderada:.2f}")
# Cálculo manual alternativo
calc_manual = sum(v * w for v, w in zip(valores, pesos)) / sum(pesos)
print(f"Cálculo manual: {calc_manual:.2f}")
Fórmula da Média Ponderada em Aplicações Reais e Específicas por Domínio
Agora que você sabe como calcular médias ponderadas, vamos explorar como elas resolvem problemas reais em diferentes áreas. Esses exemplos ajudarão você a reconhecer situações onde as médias ponderadas podem melhorar sua própria análise.
Sistema de avaliação educacional
Sistemas de avaliação acadêmica comumente usam médias ponderadas para equilibrar diferentes tipos de avaliações. Um curso típico pode pesar provas em 60%, tarefas de casa em 25% e participação em 15%.
Se um aluno tira 88 nas provas, 95 nas tarefas de casa e 92 em participação, sua nota final seria: (88×0.6) + (95×0.25) + (92×0.15) = 90.35. Esta abordagem garante que avaliações mais importantes tenham um impacto maior na nota final.
Valoração de estoque financeiro
Em aplicações de negócios, as empresas frequentemente usam o método do custo médio ponderado (CMV) para valorar o estoque quando as mercadorias são compradas a preços diferentes durante um período. Diferente de uma média aritmética simples, o CMV incorpora quantidades de compra, o que suaviza as flutuações de preço e fornece uma base de custo consistente para relatórios financeiros.
Por exemplo, se uma empresa compra 100 unidades a $10 e 300 unidades a $12, o custo médio ponderado é $11.50, não $11.00 como uma média simples sugeriria.
Análise financeira
Em finanças, as médias ponderadas vão muito além do estoque. A gestão de carteiras depende delas para calcular retornos e riscos esperados, com o peso de cada ativo baseado em sua proporção do valor total da carteira. Isso garante que participações maiores tenham mais influência do que as menores.
Da mesma forma, o Custo Médio Ponderado de Capital (WACC) aplica o mesmo princípio: ele representa o custo médio de financiamento de uma empresa ponderando os custos da dívida e do patrimônio líquido em proporção à sua participação na estrutura de capital. O WACC é um insumo chave em modelos de avaliação e decisões de investimento, pois serve como a taxa mínima de retorno da empresa.
Pesquisas estatísticas
No mundo da pesquisa, a análise de pesquisas usa médias ponderadas para ajustar desequilíbrios demográficos e garantir resultados representativos. Se sua pesquisa sub-amostra certos grupos etários, você pode ponderar as respostas para corresponder à distribuição real da população.
Este ajuste ajuda a eliminar o viés de amostragem e produz insights mais precisos sobre a população mais ampla que você está estudando.
Contabilidade de estoque
Voltando às aplicações práticas de negócios, o método da média móvel na contabilidade de estoque usa médias ponderadas para determinar o custo das mercadorias vendidas. Cada nova compra atualiza o custo médio por unidade com base no estoque remanescente e nas novas adições.
Esta abordagem suaviza a volatilidade de preços e fornece estimativas de custo estáveis para relatórios financeiros, facilitando o acompanhamento das tendências de lucratividade ao longo do tempo.
Entradas de construção ponderadas por área e outros contextos especializados
Além dessas aplicações comuns, aplicações de engenharia frequentemente usam médias ponderadas por área para cálculos de energia de edifícios, onde diferentes zonas contribuem para o desempenho geral do edifício com base em seu tamanho.
Conceitos semelhantes aparecem em sistemas de informação geográfica (GIS) para análise espacial e na manufatura para controle de qualidade em diferentes áreas de produção.
Análise Comparativa com Outras Médias
Com todas essas aplicações em mente, você pode estar se perguntando como escolher entre médias ponderadas e outros métodos de média. Entender essas distinções ajudará você a selecionar a abordagem certa para sua situação específica.
Média aritmética vs. média ponderada
Médias aritméticas assumem que todos os pontos de dados são igualmente importantes e representativos. Médias ponderadas explicitamente levam em conta diferenças em importância, confiabilidade ou frequência entre os pontos de dados.
Escolha médias ponderadas quando seus dados naturalmente têm diferentes níveis de significância ou quando você precisa ajustar para desequilíbrios de amostragem. Use médias aritméticas simples quando todos os pontos de dados realmente merecem consideração igual.
Média geométrica
Médias geométricas funcionam melhor para dados multiplicativos, como taxas de crescimento ou razões, onde você quer encontrar a taxa média de mudança ao longo do tempo. No entanto, médias geométricas não acomodam naturalmente ponderação.
Embora você possa criar médias geométricas ponderadas usando logaritmos, esta abordagem é matematicamente complexa e menos intuitiva do que médias aritméticas ponderadas para a maioria das aplicações.
Vantagens e Desvantagens das Médias Ponderadas
Antes de mergulhar em tópicos mais avançados, vale a pena dar um passo atrás para considerar as compensações mais amplas envolvidas no uso de médias ponderadas.
Prós das médias ponderadas
Médias ponderadas fornecem precisão superior quando os pontos de dados naturalmente variam em importância ou confiabilidade. Elas oferecem flexibilidade para ajustar cálculos com base no conhecimento do domínio e podem representar melhor cenários do mundo real onde nem todas as observações são iguais.
Esta abordagem se destaca em situações que exigem ajustes demográficos, análise de carteira ou qualquer contexto onde os tamanhos das amostras ou a confiança da medição variam entre os pontos de dados.
Contras das médias ponderadas
A principal limitação é a subjetividade na seleção de pesos, o que pode introduzir viés se feito de forma inadequada. Médias ponderadas também são mais sensíveis a valores atípicos com pesos altos e propensas a erros se os pesos forem atribuídos incorretamente.
Além disso, elas exigem mais esforço computacional e expertise de domínio em comparação com médias simples, tornando-as desnecessariamente complexas para situações onde a ponderação igual é apropriada.
Extensões Mais Avançadas e Teóricas
Para leitores interessados em ir além das aplicações básicas, as médias ponderadas se estendem para um território matemático mais sofisticado que abre possibilidades analíticas adicionais.
Médias ponderadas contínuas
Médias ponderadas podem se estender para funções contínuas






