主なポイント:
- Excelで加重平均を計算することは、正確な財務分析、学業評価、在庫評価に不可欠ですが、
SUMPRODUCTのような従来の数式にはExcelの技術的知識が必要です。 - Excelmaticは、シンプルな言語コマンドで加重平均を計算できるようにすることで、複雑な数式を暗記する必要をなくします。
- 手動の数式方法と比較して、Excelmaticは複雑な複数条件の計算を瞬時に処理し、エラーを減らし貴重な時間を節約します。
- マーケティング、セールス、オペレーションのビジネスプロフェッショナルにとって、ExcelmaticのようなAIツールを採用することは、技術的な実装ではなくデータの洞察に集中することを意味します。
加重平均は、GPAの計算からポートフォリオのリターンの決定まで、データ分析のあらゆる場面で登場します。すべてのデータポイントを平等に扱う単純平均とは異なり、加重平均は一部の値が他の値よりも大きな影響力を持つべきであることを認識します。これは、重要性や頻度が異なるデータを扱うときに非常に便利です。
加重平均とは?
加重平均は、事前に決められた重みに基づいて、個々のデータポイントに異なるレベルの重要性を割り当てます。単純平均はすべての値を平等に扱いますが、加重平均は最終結果を計算する前に各値に対応する重みを掛けます。
重要な洞察は次の通りです:重みは、各データポイントが最終的な平均にどれだけ影響を与えるかを直接制御します。重みの高いデータポイントは結果をその値に近づけ、重みの低いポイントは影響が少なくなります。これにより、計算をはるかに細かく制御でき、多くの場合、より意味のある結果が得られます。
加重平均は、すべてのポイントが等しく重要であると仮定するのではなく、各データポイントの相対的な重要性を考慮するという点で、単純平均と異なります。
加重平均の数式を理解する
加重平均とは何か、なぜ重要なのかを確認したので、その仕組みを支える数学的基礎について詳しく見ていきましょう。
数学的定義と基本原理
加重平均の数式は、各データポイントと対応する重みを組み合わせます:
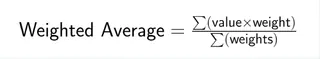
ここで、Σはすべての項の合計を表します。各値にその重みが掛けられ、これらの積をすべて合計し、すべての重みの合計で割ります。
ほとんどの実用的な文脈(確率、頻度、シェア)では、重みは非負であり、しばしば合計が1(または総数)になるように正規化されます。特殊な方法では負の重みが現れることもありますが、直感に反する結果を生む可能性があり、注意して使用する必要があります。ゼロ除算を避けるため、常に重みの合計がゼロより大きいことを確認してください。
この数式により、重みの高い値が最終結果に比例して大きな影響を与えることが保証されます。例えば、あるデータポイントの重みが10で、別のポイントの重みが1の場合、最初のポイントは最終的な平均に10倍多く寄与します。
正規化と特殊なケース
正規化とは、重みの合計が1になるようにスケーリングすることで、各重みをパーセンテージの寄与として直接解釈できるようにすることです。$(sum_i w_i = 1)$ の場合、加重平均は $(sum_i w_i x_i)$ に簡略化されます。確率の文脈では、これらの重みは確率であり、加重平均は期待値となります。
この正規化されたアプローチは、重みが合計1になる確率を表す確率の文脈で特に有用です。このような場合、加重平均は分布の期待値になります。
加重平均を使用する理由とタイミング
数学的な基礎を理解したところで、単純平均よりも加重平均の方が良い選択肢になるのはいつなのか疑問に思うかもしれません。その答えは、データが自然に異なるレベルの重要性を持っている場合を認識することにあります。
データポイントが自然に異なるレベルの重要性や頻度を持つ場合、加重平均は不可欠になります。データポイントが異なるサンプルサイズ、期間、または信頼性のレベルを表す場合、加重平均は単純平均よりも優れた働きをします。例えば、異なるクラスサイズにわたる平均テストスコアを計算する場合、大きなクラスは小さなクラスよりも全体の平均に大きな影響を与えるべきです。
加重平均は、財務計算(ポートフォリオリターン)、学業評価(異なる課題の重み付け)、調査分析(人口統計学的調整)、在庫管理(異なる購入数量にわたる原価平均)で特に価値があります。
加重平均に関する一般的な課題
加重平均は強力なツールですが、慎重に回避したい潜在的な落とし穴も伴います。
重みの選択
最も重要な課題は、適切な重みを選択することにあり、これは各データポイントが何を表すかを慎重に考慮し、ドメイン知識を必要とします。不適切な重みの選択は結果を劇的に歪め、誤解を招く結論につながる可能性があります。
例えば、顧客満足度スコアを計算していて、誤って信頼性の低いデータソースに高い重みを割り当てた場合、最終的な平均は真の顧客センチメントを正確に反映しません。常に重みが各データポイントの実際の重要性や信頼性を反映していることを確認してください。
計算上の落とし穴
重みの選択以外にも、一般的な計算エラーには、ゼロの重みの使用(データポイントを除去する)、負の重みの使用(直感に反する結果を生む可能性がある)、必要なときに重みを正規化するのを忘れることが含まれます。すべての重みがゼロの場合、ゼロ除算が発生します。
特に合計100%になるべきパーセンテージベースの重みを扱う場合は、重みの割り当てを必ず再確認し、適切な正規化を確保してください。
加重平均の計算方法:Excel、AI、Python
理論と潜在的な課題をカバーしたので、実践的な側面に目を向けましょう。加重平均の計算は、従来の数式から最新のAI搭載ツールまで、いくつかの方法で行うことができます。
方法1:従来のExcelの方法(数式を使用)
Excelは、SUMPRODUCT()関数とSUM()関数を使用して加重平均の計算を簡単に行います。SUMPRODUCTは、指定された配列内の対応する要素を乗算し、それらの積の合計を返します。
数式の構造は次の通りです:
=SUMPRODUCT(values, weights)/SUM(weights)
例えば、値がセルA2:A6にあり、対応する重みがB2:B6にある場合、数式は次のようになります:
=SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6)
この方法は信頼性がありますが、正しい関数を知り、セル範囲が正確であることを確認する必要があります。大規模または動的なデータセットの場合、これらの数式を管理することは面倒になる可能性があります。
方法2:最新のAIの方法(Excelmaticを使用)
より速く、より直感的なアプローチは、ExcelmaticのようなAI Excelエージェントを使用することです。数式を書く代わりに、平易な言語でリクエストを述べるだけで済みます。Excelmaticは、リクエストの解釈から計算の実行まで、残りの部分を処理します。
仕組みは次の通りです:
- 値と重みを含むExcelファイルをアップロードします。
- 平易な言語で質問します。
同じ例の場合、次のように尋ねるだけです:
列Aの値の加重平均を、列Bの重みを使用して計算してください。
Excelmaticはデータを瞬時に処理し、答えを提供します。数式を覚えたり、セル参照を心配したりする必要はありません。
比較:従来の数式 vs AIエージェント
| 特徴 | 従来のExcel (SUMPRODUCT) | AI搭載Excelmatic |
|---|---|---|
| 労力 | SUMPRODUCTおよびSUM関数と正しい構文の知識が必要。 |
平易な言語で尋ねるだけ。数式は不要。 |
| 速度 | 経験豊富なユーザーには速いが、タイプミスや範囲エラーが発生しやすい。 | 瞬時。AIがすべてのバックエンド計算を処理する。 |
| 柔軟性 | 固定されている。データ範囲が変更された場合、数式を手動で更新する必要がある。 | 非常に柔軟。AIは文脈を理解し、新しい質問に適応する。 |
| 学習曲線 | 中程度。特定のExcel関数を学び、覚える必要がある。 | 事実上ゼロ。質問できれば使用できる。 |
ExcelmaticのようなAIツールを使用することは、プロセスを簡素化するだけでなく、人的ミスの可能性を減らし、分析をより速く、より正確にします。
方法3:Pythonで加重平均を計算する方法
Pythonで作業している人にとって、NumPyライブラリはエレガントなソリューションを提供しますが、手動で加重平均を計算することもできます:
import numpy as np
# 値と重みを定義
values = [85, 92, 78, 95]
weights = [0.2, 0.3, 0.25, 0.25]
# 加重平均を計算
weighted_avg = np.average(values, weights=weights)
print(f"加重平均: {weighted_avg:.2f}")
# 代替の手動計算
manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)
print(f"手動計算: {manual_calc:.2f}")
実際のドメイン固有のアプリケーションにおける加重平均の数式
加重平均の計算方法がわかったので、さまざまな分野で実際の問題をどのように解決するかを探ってみましょう。これらの例は、加重平均があなた自身の分析を改善できる状況を認識するのに役立ちます。
教育評価システム
学業評価システムでは、通常、異なる種類の評価をバランスさせるために加重平均が使用されます。典型的なコースでは、試験を60%、宿題を25%、参加を15%と重み付けするかもしれません。
学生が試験で88点、宿題で95点、参加で92点を取った場合、最終成績は次のようになります:(88×0.6) + (95×0.25) + (92×0.15) = 90.35。このアプローチにより、より重要な評価が最終成績に大きな影響を与えることが保証されます。
財務在庫評価
ビジネスアプリケーションでは、企業は期間中に異なる価格で購入された商品の在庫を評価するために、加重平均原価(WAC)法を使用することがよくあります。単純な算術平均とは異なり、WACは購入数量を組み込み、価格変動を平滑化し、財務報告のための一貫した原価基準を提供します。
例えば、企業が100単位を10ドルで、300単位を12ドルで購入した場合、加重平均原価は11.50ドルであり、単純平均が示唆する11.00ドルではありません。
財務分析
財務では、加重平均は在庫をはるかに超えて拡張されます。ポートフォリオ管理は、各資産の重みが総ポートフォリオ価値に占める割合に基づいて、期待リターンとリスクを計算するためにそれらに依存します。これにより、大きな保有額が小さな保有額よりも大きな影響力を持つことが保証されます。
同様に、加重平均資本コスト(WACC)も同じ原則を適用します:それは、資本構造における負債と株式のコストをそのシェアの割合で重み付けすることにより、企業の平均的な資金調達コストを表します。WACCは、企業のリターンを生み出すためのハードルレートとして機能するため、評価モデルと投資決定における重要なインプットです。
統計調査
研究の世界では、調査分析は人口統計学的な不均衡を調整し、代表的な結果を確保するために加重平均を使用します。調査が特定の年齢層を過小サンプリングしている場合、実際の人口分布に合わせて回答に重みを付けることができます。
この調整は、サンプリングバイアスを排除し、研究対象のより広い人口についてより正確な洞察を生み出すのに役立ちます。
在庫会計
実用的なビジネスアプリケーションに戻ると、在庫会計における移動平均法は、売上原価を決定するために加重平均を使用します。新しい購入ごとに、残存在庫と新規追加に基づいて単位あたりの平均原価が更新されます。
このアプローチは価格変動を平滑化し、財務報告のための安定した原価見積もりを提供し、時間の経過に伴う収益性の傾向を追跡しやすくします。
面積加重建物インプットおよびその他の専門的な文脈
これらの一般的なアプリケーションを超えて、エンジニアリングアプリケーションでは、建物のエネルギー計算に面積加重平均を使用することが多く、異なるゾーンがそのサイズに基づいて建物全体の性能に寄与します。
同様の概念は、空間分析のための地理情報システム(GIS)や、異なる生産エリアにわたる品質管理のための製造業にも現れます。
他の平均との比較分析
これらすべてのアプリケーションを念頭に置いて、加重平均と他の平均化方法のどちらを選ぶべきか疑問に思うかもしれません。これらの違いを理解することで、特定の状況に適したアプローチを選択するのに役立ちます。
算術平均 vs 加重平均
算術平均は、すべてのデータポイントが等しく重要で代表的であると仮定します。加重平均は、データポイント間の重要性、信頼性、または頻度の違いを明示的に考慮します。
データが自然に異なるレベルの重要性を持つ場合、またはサンプリングの不均衡を調整する必要がある場合には加重平均を選択してください。すべてのデータポイントが本当に平等な考慮に値する場合には、単純な算術平均を使用してください。
幾何平均
幾何平均は、成長率や比率などの乗法的データに最適であり、時間の経過に伴う平均変化率を見つけたい場合に適しています。ただし、幾何平均は自然に重み付けに対応しません。
対数を使用して加重幾何平均を作成することはできますが、このアプローチは数学的に複雑で、ほとんどのアプリケーションでは加重算術平均よりも直感的ではありません。
加重平均の長所と短所
より高度なトピックに飛び込む前に、加重平均を使用することに伴うより広範なトレードオフを考慮する価値があります。
加重平均の長所
データポイントが自然に重要性や信頼性が異なる場合、加重平均は優れた精度を提供します。ドメイン知識に基づいて計算を調整する柔軟性を提供し、すべての観測が等しくない現実のシナリオをよりよく表現できます。
このアプローチは、人口統計学的調整、ポートフォリオ分析、またはサンプルサイズや測定信頼性がデータポイント間で異なる状況で優れています。
加重平均の短所
主な制限は、重み選択における主観性であり、不適切に行われるとバイアスを導入する可能性があります。加重平均は、重みの高い外れ値に対してより敏感であり、重みが誤って割り当てられた場合、エラーが発生しやすいです。
さらに、単純平均と比較して、より多くの計算労力とドメイン知識を必要とし、等しい重み付けが適切な状況では不必要に複雑になります。
より高度で理論的な拡張
基本的なアプリケーションを超えて進みたい読者のために、加重平均は追加の分析的可能性を開くより洗練された数学的領域に拡張されます。
連続加重平均
加重平均は、積分計算を使用して連続関数に拡張できます。離散的な重みと値の代わりに、連続的な重みと値の関数を積分します:






