Points clés :
- Le calcul des moyennes pondérées dans Excel est essentiel pour une analyse financière précise, l'évaluation académique et la valorisation des stocks, mais les formules traditionnelles comme
SOMMEPRODnécessitent des connaissances techniques en Excel. - Excelmatic élimine le besoin de mémoriser des formules complexes en vous permettant de calculer des moyennes pondérées à l'aide de commandes en langage simple.
- Comparé aux méthodes manuelles avec formules, Excelmatic gère instantanément des calculs complexes à plusieurs critères, réduisant les erreurs et économisant un temps précieux.
- Pour les professionnels du marketing, des ventes et des opérations, adopter des outils d'IA comme Excelmatic signifie se concentrer sur les insights des données plutôt que sur la mise en œuvre technique.
Les moyennes pondérées apparaissent partout dans l'analyse de données, du calcul de votre moyenne générale à la détermination des rendements d'un portefeuille. Contrairement aux moyennes simples qui traitent tous les points de données de manière égale, les moyennes pondérées reconnaissent que certaines valeurs méritent plus d'influence que d'autres. Cela les rend incroyablement utiles lorsque vous traitez des données d'importance ou de fréquence variables.
Qu'est-ce qu'une moyenne pondérée ?
Une moyenne pondérée attribue différents niveaux d'importance à chaque point de données en fonction de poids prédéterminés. Alors qu'une moyenne simple traite toutes les valeurs de manière égale, une moyenne pondérée multiplie chaque valeur par son poids correspondant avant de calculer le résultat final.
Voici l'idée clé : les poids contrôlent directement l'influence de chaque point de données sur la moyenne finale. Un point de données avec un poids plus élevé rapproche le résultat de sa valeur, tandis que les points avec un poids plus faible ont moins d'impact. Cela vous donne beaucoup plus de contrôle sur vos calculs et produit souvent des résultats plus significatifs.
Les moyennes pondérées diffèrent des moyennes simples sur un point important : elles tiennent compte de l'importance relative de chaque point de données plutôt que de supposer que tous les points sont également importants.
Comprendre la formule de la moyenne pondérée
Maintenant que nous avons établi ce que sont les moyennes pondérées et pourquoi elles sont importantes, plongeons dans les fondements mathématiques qui les font fonctionner.
Définition mathématique et principes de base
La formule de la moyenne pondérée combine chaque point de données avec son poids correspondant :
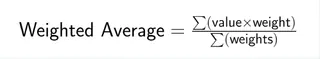
Où Σ représente la somme de tous les termes. Chaque valeur est multipliée par son poids, puis vous additionnez tous ces produits et divisez par le total de tous les poids.
Dans la plupart des contextes pratiques (probabilités, fréquences et parts), les poids sont non négatifs et souvent normalisés pour sommer à 1 (ou au nombre total). Dans des méthodes spécialisées, des poids négatifs peuvent apparaître, mais ils peuvent donner des résultats contre-intuitifs et doivent être utilisés avec prudence. Assurez-vous toujours que la somme des poids est supérieure à zéro pour éviter une division par zéro.
Cette formule garantit que les valeurs avec un poids plus élevé ont une influence proportionnellement plus grande sur le résultat final. Par exemple, si un point de données a un poids de 10 et un autre un poids de 1, le premier point contribue dix fois plus à la moyenne finale.
Normalisation et cas particuliers
La normalisation signifie mettre les poids à l'échelle pour qu'ils somment à 1, rendant chaque poids directement interprétable comme un pourcentage de contribution. Lorsque $(sum_i w_i = 1)$, la moyenne pondérée se simplifie en $(sum_i w_i x_i)$. Dans les contextes de probabilité, ces poids sont des probabilités et la moyenne pondérée est l'espérance mathématique.
Cette approche normalisée est particulièrement utile dans les contextes de probabilité, où les poids représentent des probabilités qui doivent sommer à 1. Dans ces cas, la moyenne pondérée devient l'espérance de la distribution.
Pourquoi et quand utiliser les moyennes pondérées
Avec les bases mathématiques en place, vous vous demandez peut-être quand les moyennes pondérées deviennent le meilleur choix par rapport aux moyennes simples. La réponse réside dans la reconnaissance du moment où vos données ont naturellement des niveaux de signification variables.
Les moyennes pondérées deviennent essentielles lorsque vos points de données ont naturellement des niveaux d'importance ou de fréquence différents. Vous constaterez que les moyennes pondérées fonctionnent mieux que les moyennes simples lorsque les points de données représentent des tailles d'échantillon, des périodes ou des niveaux de fiabilité différents. Par exemple, lors du calcul des scores moyens aux tests dans différentes classes, les classes plus nombreuses devraient influencer la moyenne globale plus que les classes plus petites.
Les moyennes pondérées sont particulièrement précieuses dans les calculs financiers (rendements de portefeuille), l'évaluation académique (pondérations différentes des devoirs), l'analyse d'enquêtes (ajustements démographiques) et la gestion des stocks (moyenne des coûts sur différentes quantités d'achat).
Défis courants avec les moyennes pondérées
Bien que les moyennes pondérées soient des outils puissants, elles s'accompagnent de leur propre ensemble d'écueils potentiels que vous voudrez naviguer avec soin.
Sélection des poids
Le défi le plus critique réside dans le choix de poids appropriés, ce qui nécessite une expertise du domaine et une réflexion minutieuse sur ce que représente chaque point de données. Une mauvaise sélection des poids peut fausser considérablement les résultats et conduire à des conclusions trompeuses.
Par exemple, si vous calculez des scores de satisfaction client et attribuez accidentellement des poids plus élevés à des sources de données moins fiables, votre moyenne finale ne reflétera pas avec précision le véritable sentiment des clients. Assurez-vous toujours que vos poids reflètent l'importance ou la fiabilité réelle de chaque point de données.
Pièges de calcul
Au-delà de la sélection des poids, les erreurs de calcul courantes incluent l'utilisation de poids nuls (ce qui supprime les points de données), de poids négatifs (qui peuvent produire des résultats contre-intuitifs) et l'oubli de normaliser les poids lorsque cela est nécessaire. Une division par zéro se produit lorsque tous les poids sont nuls.
Vérifiez toujours vos affectations de poids et assurez une normalisation correcte, surtout lorsque vous travaillez avec des poids en pourcentage qui devraient sommer à 100 %.
Comment calculer une moyenne pondérée : Excel, IA et Python
Après avoir couvert la théorie et les défis potentiels, passons à l'aspect pratique. Le calcul d'une moyenne pondérée peut se faire de plusieurs manières, des formules traditionnelles aux outils modernes alimentés par l'IA.
Méthode 1 : La méthode Excel traditionnelle (utilisation de formules)
Excel rend les calculs de moyenne pondérée simples en utilisant les fonctions SOMMEPROD() et SOMME(). SOMMEPROD multiplie les composants correspondants dans les tableaux donnés et renvoie la somme de ces produits.
La structure de la formule est :
=SOMMEPROD(valeurs, poids)/SOMME(poids)
Par exemple, si vos valeurs sont dans les cellules A2:A6 et leurs poids correspondants dans B2:B6, la formule serait :
=SOMMEPROD(A2:A6, B2:B6) / SOMME(B2:B6)
Cette méthode est fiable mais nécessite de connaître les bonnes fonctions et de s'assurer que vos plages de cellules sont exactes. Pour des jeux de données volumineux ou dynamiques, la gestion de ces formules peut devenir fastidieuse.
Méthode 2 : La méthode IA moderne (utilisation d'Excelmatic)
Une approche plus rapide et plus intuitive consiste à utiliser un agent Excel IA comme Excelmatic. Au lieu d'écrire des formules, vous pouvez simplement exprimer votre demande en langage clair. Excelmatic s'occupe du reste, de l'interprétation de votre demande à l'exécution du calcul.
Voici comment cela fonctionne :
- Téléchargez votre fichier Excel contenant les valeurs et les poids.
- Posez votre question en langage clair.
Pour le même exemple, vous demanderiez simplement :
Calculez la moyenne pondérée des valeurs de la colonne A en utilisant les poids de la colonne B.
Excelmatic traite instantanément vos données et fournit la réponse, éliminant le besoin de mémoriser des formules ou de s'inquiéter des références de cellules.
Comparaison : Formule traditionnelle vs. Agent IA
| Caractéristique | Excel traditionnel (SOMMEPROD) | Excelmatic alimenté par l'IA |
|---|---|---|
| Effort | Nécessite la connaissance des fonctions SOMMEPROD et SOMME et de la syntaxe correcte. |
Demandez simplement en langage clair. Aucune formule nécessaire. |
| Vitesse | Rapide pour les utilisateurs expérimentés, mais sujet aux fautes de frappe et aux erreurs de plage. | Instantané. L'IA gère tous les calculs en arrière-plan. |
| Flexibilité | Rigide. La formule doit être mise à jour manuellement si les plages de données changent. | Très flexible. L'IA comprend le contexte et s'adapte aux nouvelles questions. |
| Courbe d'apprentissage | Modérée. Vous devez apprendre et mémoriser des fonctions Excel spécifiques. | Pratiquement nulle. Si vous pouvez poser une question, vous pouvez l'utiliser. |
Utiliser un outil d'IA comme Excelmatic simplifie non seulement le processus, mais réduit aussi les risques d'erreur humaine, rendant votre analyse plus rapide et plus précise.
Méthode 3 : Comment calculer une moyenne pondérée en Python
Pour ceux qui travaillent en Python, la bibliothèque NumPy fournit une solution élégante, bien que vous puissiez aussi calculer des moyennes pondérées manuellement :
import numpy as np
# Définir les valeurs et les poids
values = [85, 92, 78, 95]
weights = [0.2, 0.3, 0.25, 0.25]
# Calculer la moyenne pondérée
weighted_avg = np.average(values, weights=weights)
print(f"Moyenne pondérée : {weighted_avg:.2f}")
# Calcul manuel alternatif
manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)
print(f"Calcul manuel : {manual_calc:.2f}")
Formule de moyenne pondérée dans des applications réelles et spécifiques à un domaine
Maintenant que vous savez comment calculer des moyennes pondérées, explorons comment elles résolvent des problèmes réels dans différents domaines. Ces exemples vous aideront à reconnaître les situations où les moyennes pondérées peuvent améliorer votre propre analyse.
Système de notation éducative
Les systèmes de notation académique utilisent couramment des moyennes pondérées pour équilibrer différents types d'évaluations. Un cours typique pourrait pondérer les examens à 60 %, les devoirs à 25 % et la participation à 15 %.
Si un étudiant obtient 88 aux examens, 95 aux devoirs et 92 à la participation, sa note finale serait : (88×0,6) + (95×0,25) + (92×0,15) = 90,35. Cette approche garantit que les évaluations les plus importantes ont un impact plus grand sur la note finale.
Valorisation des stocks financiers
Dans les applications commerciales, les entreprises utilisent souvent la méthode du coût moyen pondéré (CMP) pour valoriser les stocks lorsque des marchandises sont achetées à des prix différents pendant une période. Contrairement à une simple moyenne arithmétique, le CMP intègre les quantités achetées, ce qui lisse les fluctuations de prix et fournit une base de coût cohérente pour la comptabilité.
Par exemple, si une entreprise achète 100 unités à 10 $ et 300 unités à 12 $, le coût moyen pondéré est de 11,50 $, et non de 11,00 $ comme le suggérerait une simple moyenne.
Analyse financière
En finance, les moyennes pondérées vont bien au-delà des stocks. La gestion de portefeuille s'appuie sur elles pour calculer les rendements et les risques attendus, le poids de chaque actif étant basé sur sa proportion de la valeur totale du portefeuille. Cela garantit que les participations plus importantes ont plus d'influence que les plus petites.
De même, le Coût Moyen Pondéré du Capital (CMPC) applique le même principe : il représente le coût moyen du financement d'une entreprise en pondérant les coûts de la dette et des capitaux propres en proportion de leur part dans la structure du capital. Le CMPC est un intrant clé dans les modèles de valorisation et les décisions d'investissement, car il sert de taux de rendement minimum requis pour l'entreprise.
Enquêtes statistiques
Dans le monde de la recherche, l'analyse d'enquêtes utilise des moyennes pondérées pour ajuster les déséquilibres démographiques et garantir des résultats représentatifs. Si votre enquête sous-échantillonne certains groupes d'âge, vous pouvez pondérer les réponses pour correspondre à la distribution réelle de la population.
Cet ajustement aide à éliminer le biais d'échantillonnage et produit des insights plus précis sur la population plus large que vous étudiez.
Comptabilité des stocks
Revenant aux applications commerciales pratiques, la méthode de la moyenne mobile en comptabilité des stocks utilise des moyennes pondérées pour déterminer le coût des marchandises vendues. Chaque nouvel achat met à jour le coût moyen par unité en fonction du stock restant et des nouveaux ajouts.
Cette approche lisse la volatilité des prix et fournit des estimations de coût stables pour la comptabilité, facilitant le suivi des tendances de rentabilité au fil du temps.
Intrants de construction pondérés par la surface et autres contextes spécialisés
Au-delà de ces applications courantes, les applications d'ingénierie utilisent souvent des moyennes pondérées par la surface pour les calculs énergétiques des bâtiments, où différentes zones contribuent à la performance globale du bâtiment en fonction de leur taille.
Des concepts similaires apparaissent dans les systèmes d'information géographique (SIG) pour l'analyse spatiale et dans la fabrication pour le contrôle de la qualité dans différentes zones de production.
Analyse comparative avec d'autres moyennes
Avec toutes ces applications en tête, vous vous demandez peut-être comment choisir entre les moyennes pondérées et d'autres méthodes de calcul de moyenne. Comprendre ces distinctions vous aidera à sélectionner la bonne approche pour votre situation spécifique.
Moyenne arithmétique vs. moyenne pondérée
Les moyennes arithmétiques supposent que tous les points de données sont également importants et représentatifs. Les moyennes pondérées tiennent explicitement compte des différences d'importance, de fiabilité ou de fréquence entre les points de données.
Choisissez les moyennes pondérées lorsque vos données ont naturellement des niveaux de signification différents ou lorsque vous devez ajuster des déséquilibres d'échantillonnage. Utilisez les moyennes arithmétiques simples lorsque tous les points de données méritent vraiment une considération égale.
Moyenne géométrique
Les moyennes géométriques fonctionnent mieux pour les données multiplicatives comme les taux de croissance ou les ratios, où vous voulez trouver le taux de changement moyen dans le temps. Cependant, les moyennes géométriques n'accommodent pas naturellement la pondération.
Bien que vous puissiez créer des moyennes géométriques pondérées en utilisant des logarithmes, cette approche est mathématiquement complexe et moins intuitive que les moyennes arithmétiques pondérées pour la plupart des applications.
Avantages et inconvénients des moyennes pondérées
Avant de plonger dans des sujets plus avancés, il vaut la peine de prendre du recul pour considérer les compromis plus larges impliqués dans l'utilisation des moyennes pondérées.
Avantages des moyennes pondérées
Les moyennes pondérées offrent une précision supérieure lorsque les points de données ont naturellement une importance ou une fiabilité variable. Elles offrent la flexibilité d'ajuster les calculs en fonction des connaissances du domaine et peuvent mieux représenter des scénarios réels où toutes les observations ne sont pas égales.
Cette approche excelle dans les situations nécessitant des ajustements démographiques, l'analyse de portefeuille ou tout contexte où la taille des échantillons ou la confiance dans la mesure varie selon les points de données.






