Puntos Clave:
- Calcular promedios ponderados en Excel es esencial para un análisis financiero preciso, calificaciones académicas y valoración de inventario, pero fórmulas tradicionales como
SUMPRODUCTrequieren conocimientos técnicos de Excel. - Excelmatic elimina la necesidad de memorizar fórmulas complejas al permitirte calcular promedios ponderados usando comandos simples en lenguaje natural.
- En comparación con los métodos manuales de fórmulas, Excelmatic maneja cálculos complejos con múltiples criterios al instante, reduciendo errores y ahorrando tiempo valioso.
- Para profesionales de negocios en marketing, ventas y operaciones, adoptar herramientas de IA como Excelmatic significa enfocarse en los insights de los datos en lugar de en la implementación técnica.
Los promedios ponderados aparecen en todas partes del análisis de datos, desde calcular tu GPA hasta determinar los rendimientos de una cartera. A diferencia de los promedios simples que tratan todos los puntos de datos por igual, los promedios ponderados reconocen que algunos valores merecen más influencia que otros. Esto los hace increíblemente útiles cuando trabajas con datos de importancia o frecuencia variable.
¿Qué es un Promedio Ponderado?
Un promedio ponderado asigna diferentes niveles de importancia a puntos de datos individuales basándose en pesos predeterminados. Mientras que un promedio simple trata todos los valores por igual, un promedio ponderado multiplica cada valor por su peso correspondiente antes de calcular el resultado final.
Aquí está la idea clave: los pesos controlan directamente cuánto influye cada punto de datos en el promedio final. Un punto de datos con un peso más alto acerca el resultado a su valor, mientras que los puntos con pesos más bajos tienen menos impacto. Esto te da mucho más control sobre tus cálculos y a menudo produce resultados más significativos.
Los promedios ponderados difieren de los promedios simples en un aspecto importante: tienen en cuenta la importancia relativa de cada punto de datos en lugar de asumir que todos son igualmente importantes.
Comprendiendo la Fórmula del Promedio Ponderado
Ahora que hemos establecido qué son los promedios ponderados y por qué importan, profundicemos en los fundamentos matemáticos que los hacen funcionar.
Definición matemática y principios básicos
La fórmula del promedio ponderado combina cada punto de datos con su peso correspondiente:
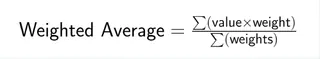
Donde Σ representa la suma de todos los términos. Cada valor se multiplica por su peso, luego sumas todos estos productos y divides por el total de todos los pesos.
En la mayoría de los contextos prácticos (probabilidades, frecuencias y participaciones), los pesos son no negativos y a menudo se normalizan para sumar 1 (o el total). En métodos especializados, pueden aparecer pesos negativos, pero pueden dar resultados contraintuitivos y deben usarse con cuidado. Siempre asegúrate de que la suma de los pesos sea mayor que cero para evitar la división por cero.
Esta fórmula garantiza que los valores con mayor peso tengan una influencia proporcionalmente mayor en el resultado final. Por ejemplo, si un punto de datos tiene un peso de 10 y otro tiene un peso de 1, el primer punto contribuye diez veces más al promedio final.
Normalización y casos especiales
La normalización significa escalar los pesos para que sumen 1, haciendo que cada peso sea directamente interpretable como un porcentaje de contribución. Cuando $(sum_i w_i = 1)$, el promedio ponderado se simplifica a $(sum_i w_i x_i)$. En contextos de probabilidad, estos pesos son probabilidades y el promedio ponderado es el valor esperado.
Este enfoque normalizado es especialmente útil en contextos de probabilidad, donde los pesos representan probabilidades que deben sumar 1. En estos casos, el promedio ponderado se convierte en el valor esperado de la distribución.
Por qué y Cuándo Usar Promedios Ponderados
Con los fundamentos matemáticos establecidos, quizás te preguntes cuándo los promedios ponderados se convierten en la mejor opción sobre los promedios simples. La respuesta está en reconocer cuándo tus datos tienen naturalmente diferentes niveles de importancia.
Los promedios ponderados se vuelven esenciales cuando tus puntos de datos tienen naturalmente diferentes niveles de importancia o frecuencia. Encontrarás que los promedios ponderados funcionan mejor que los promedios simples cuando los puntos de datos representan diferentes tamaños de muestra, períodos de tiempo o niveles de confiabilidad. Por ejemplo, al calcular puntajes promedio de exámenes en diferentes tamaños de clase, las clases más grandes deberían influir más en el promedio general que las más pequeñas.
Los promedios ponderados son particularmente valiosos en cálculos financieros (rendimientos de cartera), calificaciones académicas (diferentes pesos de tareas), análisis de encuestas (ajustes demográficos) y gestión de inventario (promedio de costos en diferentes cantidades de compra).
Desafíos Comunes con los Promedios Ponderados
Si bien los promedios ponderados son herramientas poderosas, vienen con su propio conjunto de posibles dificultades que querrás navegar con cuidado.
Selección de pesos
El desafío más crítico radica en elegir pesos apropiados, lo que requiere experiencia en el dominio y una consideración cuidadosa de lo que representa cada punto de datos. Una mala selección de pesos puede sesgar los resultados drásticamente y llevar a conclusiones engañosas.
Por ejemplo, si estás calculando puntajes de satisfacción del cliente y accidentalmente asignas pesos más altos a fuentes de datos menos confiables, tu promedio final no reflejará con precisión el sentimiento real del cliente. Siempre asegúrate de que tus pesos reflejen la importancia o confiabilidad real de cada punto de datos.
Dificultades computacionales
Más allá de la selección de pesos, los errores computacionales comunes incluyen usar pesos cero (que elimina puntos de datos), pesos negativos (que pueden producir resultados contraintuitivos) y olvidar normalizar los pesos cuando es necesario. La división por cero ocurre cuando todos los pesos son cero.
Siempre verifica dos veces tus asignaciones de pesos y asegúrate de una normalización adecuada, especialmente cuando trabajas con pesos basados en porcentajes que deberían sumar 100%.
Cómo Calcular el Promedio Ponderado: Excel, IA y Python
Habiendo cubierto la teoría y los desafíos potenciales, pasemos al lado práctico. Calcular un promedio ponderado se puede hacer de varias maneras, desde fórmulas tradicionales hasta modernas herramientas impulsadas por IA.
Método 1: El Método Tradicional de Excel (Usando Fórmulas)
Excel hace que los cálculos de promedio ponderado sean sencillos usando las funciones SUMPRODUCT() y SUM(). SUMPRODUCT multiplica los componentes correspondientes en los arreglos dados y devuelve la suma de esos productos.
La estructura de la fórmula es:
=SUMPRODUCT(valores, pesos)/SUM(pesos)
Por ejemplo, si tus valores están en las celdas A2:A6 y sus pesos correspondientes están en B2:B6, la fórmula sería:
=SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6)
Este método es confiable pero requiere que conozcas las funciones correctas y asegures que tus rangos de celdas sean precisos. Para conjuntos de datos grandes o dinámicos, gestionar estas fórmulas puede volverse engorroso.
Método 2: El Método Moderno de IA (Usando Excelmatic)
Un enfoque más rápido e intuitivo es usar un Agente de IA para Excel como Excelmatic. En lugar de escribir fórmulas, simplemente puedes expresar tu solicitud en lenguaje natural. Excelmatic se encarga del resto, desde interpretar tu solicitud hasta realizar el cálculo.
Así es como funciona:
- Sube tu archivo de Excel que contiene los valores y pesos.
- Haz tu pregunta en lenguaje natural.
Para el mismo ejemplo, simplemente preguntarías:
Calcula el promedio ponderado de los valores en la columna A usando los pesos en la columna B.
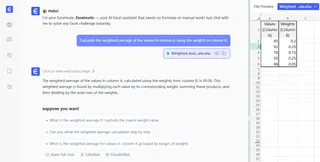
Excelmatic procesa instantáneamente tus datos y proporciona la respuesta, eliminando la necesidad de recordar fórmulas o preocuparse por las referencias de celdas.
Comparación: Fórmula Tradicional vs. Agente de IA
| Característica | Excel Tradicional (SUMPRODUCT) | Excelmatic Impulsado por IA |
|---|---|---|
| Esfuerzo | Requiere conocimiento de las funciones SUMPRODUCT y SUM y la sintaxis correcta. |
Solo pregunta en lenguaje natural. No se necesitan fórmulas. |
| Velocidad | Rápido para usuarios experimentados, pero propenso a errores tipográficos y de rango. | Instantáneo. La IA maneja todos los cálculos en segundo plano. |
| Flexibilidad | Rígida. La fórmula debe actualizarse manualmente si cambian los rangos de datos. | Muy flexible. La IA entiende el contexto y se adapta a nuevas preguntas. |
| Curva de Aprendizaje | Moderada. Necesitas aprender y recordar funciones específicas de Excel. | Prácticamente cero. Si puedes hacer una pregunta, puedes usarlo. |
Usar una herramienta de IA como Excelmatic no solo simplifica el proceso, sino que también reduce la posibilidad de error humano, haciendo tu análisis más rápido y preciso.
Método 3: Cómo Calcular el Promedio Ponderado en Python
Para aquellos que trabajan en Python, la biblioteca NumPy proporciona una solución elegante, aunque también puedes calcular promedios ponderados manualmente:
import numpy as np
# Definir valores y pesos
values = [85, 92, 78, 95]
weights = [0.2, 0.3, 0.25, 0.25]
# Calcular promedio ponderado
weighted_avg = np.average(values, weights=weights)
print(f"Promedio ponderado: {weighted_avg:.2f}")
# Cálculo manual alternativo
manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)
print(f"Cálculo manual: {manual_calc:.2f}")
Fórmula del Promedio Ponderado en Aplicaciones Reales y Específicas por Dominio
Ahora que sabes cómo calcular promedios ponderados, exploremos cómo resuelven problemas reales en diferentes campos. Estos ejemplos te ayudarán a reconocer situaciones donde los promedios ponderados pueden mejorar tu propio análisis.
Sistema de calificación educativa
Los sistemas de calificación académica comúnmente usan promedios ponderados para equilibrar diferentes tipos de evaluaciones. Un curso típico podría ponderar los exámenes en un 60%, las tareas en un 25% y la participación en un 15%.
Si un estudiante obtiene 88 en exámenes, 95 en tareas y 92 en participación, su calificación final sería: (88×0.6) + (95×0.25) + (92×0.15) = 90.35. Este enfoque asegura que las evaluaciones más importantes tengan un mayor impacto en la calificación final.
Valoración de inventario financiero
En aplicaciones empresariales, las empresas a menudo usan el método del costo promedio ponderado (CPP) para valorar el inventario cuando los bienes se compran a diferentes precios durante un período. A diferencia de una media aritmética simple, el CPP incorpora las cantidades de compra, lo que suaviza las fluctuaciones de precios y proporciona una base de costo consistente para los informes financieros.
Por ejemplo, si una empresa compra 100 unidades a $10 y 300 unidades a $12, el costo promedio ponderado es $11.50, no $11.00 como sugeriría un promedio simple.
Análisis financiero
En finanzas, los promedios ponderados se extienden mucho más allá del inventario. La gestión de carteras depende de ellos para calcular los rendimientos y riesgos esperados, donde el peso de cada activo se basa en su proporción del valor total de la cartera. Esto asegura que las tenencias más grandes tengan más influencia que las más pequeñas.
De manera similar, el Costo Promedio Ponderado del Capital (WACC) aplica el mismo principio: representa el costo promedio de financiamiento de una empresa ponderando los costos de la deuda y el capital en proporción a su participación en la estructura de capital. El WACC es un insumo clave en los modelos de valoración y las decisiones de inversión, ya que sirve como la tasa mínima de rentabilidad de la empresa para generar rendimientos.
Encuestas estadísticas
En el mundo de la investigación, el análisis de encuestas usa promedios ponderados para ajustar los desequilibrios demográficos y asegurar resultados representativos. Si tu encuesta submuestrea ciertos grupos de edad, puedes ponderar las respuestas para que coincidan con la distribución real de la población.
Este ajuste ayuda a eliminar el sesgo de muestreo y produce insights más precisos sobre la población más amplia que estás estudiando.
Contabilidad de inventario
Volviendo a las aplicaciones empresariales prácticas, el método del promedio móvil en la contabilidad de inventario usa promedios ponderados para determinar el costo de los bienes vendidos. Cada nueva compra actualiza el costo promedio por unidad basándose en el inventario restante y las nuevas adiciones.
Este enfoque suaviza la volatilidad de los precios y proporciona estimaciones de costos estables para los informes financieros, facilitando el seguimiento de las tendencias de rentabilidad a lo largo del tiempo.
Entradas de construcción ponderadas por área y otros contextos especializados
Más allá de estas aplicaciones comunes, las aplicaciones de ingeniería a menudo usan promedios ponderados por área para cálculos de energía en edificios, donde diferentes zonas contribuyen al rendimiento general del edificio según su tamaño.
Conceptos similares aparecen en los sistemas de información geográfica (SIG) para el análisis espacial y en la fabricación para el control de calidad en diferentes áreas de producción.
Análisis Comparativo con Otros Promedios
Con todas estas aplicaciones en mente, quizás te preguntes cómo elegir entre promedios ponderados y otros métodos de promediación. Comprender estas distinciones te ayudará a seleccionar el enfoque correcto para tu situación específica.
Media aritmética vs. media ponderada
Las medias aritméticas asumen que todos los puntos de datos son igualmente importantes y representativos. Los promedios ponderados tienen en cuenta explícitamente las diferencias en importancia, confiabilidad o frecuencia entre los puntos de datos.
Elige promedios ponderados cuando tus datos tengan naturalmente diferentes niveles de importancia o cuando necesites ajustar por desequilibrios de muestreo. Usa medias aritméticas simples cuando todos los puntos de datos realmente merezcan una consideración igual.
Media geométrica
Las medias geométricas funcionan mejor para datos multiplicativos como tasas de crecimiento o proporciones, donde quieres encontrar la tasa de cambio promedio a lo largo del tiempo. Sin embargo, las medias geométricas no acomodan naturalmente la ponderación.
Si bien puedes crear medias geométricas ponderadas usando logaritmos, este enfoque es matemáticamente complejo y menos intuitivo que las medias aritméticas ponderadas para la mayoría de las aplicaciones.
Ventajas y Desventajas de los Promedios Ponderados
Antes de profundizar en temas más avanzados, vale la pena dar un paso atrás para considerar las compensaciones más amplias involucradas en el uso de promedios ponderados.
Pros de los promedios ponderados
Los promedios ponderados proporcionan una precisión superior cuando los puntos de datos varían naturalmente en importancia o confiabilidad. Ofrecen flexibilidad para ajustar los cálculos basándose en el conocimiento del dominio y pueden representar mejor escenarios del mundo real donde no todas las observaciones son iguales.
Este enfoque sobresale en situaciones que requieren ajustes demográficos, análisis de cartera o cualquier contexto donde el tamaño de la muestra o la confianza en la medición varíe entre los puntos de datos.
Contras de los promedios ponderados
La principal limitación es la subjetividad en la selección de pesos, lo que puede introducir sesgos si se hace mal. Los promedios ponderados también son más sensibles a los valores atípicos con pesos altos y propensos a errores si los pesos se asignan incorrectamente.
Además, requieren más esfuerzo computacional y experiencia en el dominio en comparación con los promedios simples, lo que los hace innecesariamente complejos para situaciones donde la ponderación igual es apropiada.
Extensiones Teóricas y Más Avanzadas
Para los lectores interesados en ir más allá de las aplicaciones básicas, los promedios ponderados se extienden a un territorio matemático más sofisticado que abre posibilidades analíticas adicionales.
Promedios ponderados continuos
Los promedios ponderados pueden extenderse a funciones continuas usando cálculo integral. En lugar de pesos y valores discretos, integ






