Wichtige Erkenntnisse:
- Die Berechnung gewichteter Durchschnitte in Excel ist für genaue Finanzanalysen, akademische Benotung und Lagerbewertung unerlässlich, aber traditionelle Formeln wie
SUMPRODUCTerfordern technisches Excel-Wissen. - Excelmatic macht das Auswendiglernen komplexer Formeln überflüssig, indem es Ihnen ermöglicht, gewichtete Durchschnitte mit einfachen Sprachbefehlen zu berechnen.
- Im Vergleich zu manuellen Formelmethoden bewältigt Excelmatic komplexe Mehrkriterienberechnungen sofort, reduziert Fehler und spart wertvolle Zeit.
- Für Fachleute in Marketing, Vertrieb und Betrieb bedeutet die Einführung von KI-Tools wie Excelmatic, sich auf Dateneinblicke statt auf technische Umsetzung zu konzentrieren.
Gewichtete Durchschnitte tauchen überall in der Datenanalyse auf, von der Berechnung Ihres Notendurchschnitts bis zur Ermittlung von Portfoliorenditen. Im Gegensatz zu einfachen Durchschnitten, die alle Datenpunkte gleich behandeln, erkennen gewichtete Durchschnitte an, dass einige Werte mehr Einfluss verdienen als andere. Das macht sie unglaublich nützlich, wenn Sie mit Daten unterschiedlicher Wichtigkeit oder Häufigkeit arbeiten.
Was ist ein gewichteter Durchschnitt?
Ein gewichteter Durchschnitt weist einzelnen Datenpunkten basierend auf vorgegebenen Gewichten unterschiedliche Wichtigkeitsstufen zu. Während ein einfacher Durchschnitt alle Werte gleich behandelt, multipliziert ein gewichteter Durchschnitt jeden Wert mit seinem entsprechenden Gewicht, bevor das Endergebnis berechnet wird.
Hier ist die zentrale Einsicht: Gewichte steuern direkt, wie stark jeder Datenpunkt den endgültigen Durchschnitt beeinflusst. Ein Datenpunkt mit einem höheren Gewicht zieht das Ergebnis näher an seinen Wert heran, während Punkte mit geringerem Gewicht weniger Einfluss haben. Dies gibt Ihnen viel mehr Kontrolle über Ihre Berechnungen und liefert oft aussagekräftigere Ergebnisse.
Gewichtete Durchschnitte unterscheiden sich in einem wichtigen Punkt von einfachen Durchschnitten: Sie berücksichtigen die relative Bedeutung jedes Datenpunkts, anstatt davon auszugehen, dass alle Punkte gleich wichtig sind.
Die Formel für den gewichteten Durchschnitt verstehen
Nachdem wir nun geklärt haben, was gewichtete Durchschnitte sind und warum sie wichtig sind, tauchen wir in die mathematische Grundlage ein, die sie funktionieren lässt.
Mathematische Definition und Kernprinzipien
Die Formel für den gewichteten Durchschnitt kombiniert jeden Datenpunkt mit seinem entsprechenden Gewicht:
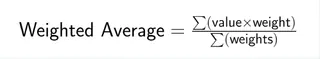
Wobei Σ die Summe aller Terme darstellt. Jeder Wert wird mit seinem Gewicht multipliziert, dann addieren Sie alle diese Produkte und teilen durch die Summe aller Gewichte.
In den meisten praktischen Kontexten (Wahrscheinlichkeiten, Häufigkeiten und Anteile) sind Gewichte nicht-negativ und oft so normalisiert, dass sie zu 1 (oder zur Gesamtzahl) summieren. In spezialisierten Methoden können negative Gewichte auftreten, aber sie können zu kontraintuitiven Ergebnissen führen und sollten mit Vorsicht verwendet werden. Stellen Sie immer sicher, dass die Summe der Gewichte größer als Null ist, um eine Division durch Null zu vermeiden.
Diese Formel stellt sicher, dass höher gewichtete Werte proportional mehr Einfluss auf das Endergebnis haben. Wenn beispielsweise ein Datenpunkt ein Gewicht von 10 und ein anderer ein Gewicht von 1 hat, trägt der erste Punkt zehnmal mehr zum endgültigen Durchschnitt bei.
Normalisierung und Sonderfälle
Normalisierung bedeutet, Gewichte so zu skalieren, dass sie zu 1 summieren, wodurch jedes Gewicht direkt als prozentualer Beitrag interpretierbar wird. Wenn $(sum_i w_i = 1)$ ist, vereinfacht sich der gewichtete Durchschnitt zu $(sum_i w_i x_i)$. In Wahrscheinlichkeitskontexten sind diese Gewichte Wahrscheinlichkeiten und der gewichtete Durchschnitt ist der Erwartungswert.
Dieser normalisierte Ansatz ist besonders nützlich in Wahrscheinlichkeitskontexten, wo Gewichte Wahrscheinlichkeiten darstellen, die zu 1 summieren müssen. In diesen Fällen wird der gewichtete Durchschnitt zum Erwartungswert der Verteilung.
Warum und wann gewichtete Durchschnitte verwendet werden sollten
Mit dem mathematischen Fundament könnten Sie sich fragen, wann gewichtete Durchschnitte die bessere Wahl gegenüber einfachen Durchschnitten sind. Die Antwort liegt darin, zu erkennen, wann Ihre Daten natürlicherweise unterschiedliche Bedeutungsebenen haben.
Gewichtete Durchschnitte werden unerlässlich, wenn Ihre Datenpunkte natürlicherweise unterschiedliche Wichtigkeits- oder Häufigkeitsstufen haben. Sie werden feststellen, dass gewichtete Durchschnitte besser funktionieren als einfache Durchschnitte, wenn Datenpunkte unterschiedliche Stichprobengrößen, Zeiträume oder Zuverlässigkeitsniveaus repräsentieren. Zum Beispiel sollten bei der Berechnung von Durchschnittstestergebnissen über verschiedene Klassengrößen hinweg größere Klassen den Gesamtdurchschnitt stärker beeinflussen als kleinere.
Gewichtete Durchschnitte sind besonders wertvoll bei Finanzberechnungen (Portfoliorenditen), akademischer Benotung (unterschiedliche Gewichtung von Aufgaben), Umfrageanalyse (demografische Anpassungen) und Bestandsverwaltung (Kostendurchschnitt über verschiedene Einkaufsmengen hinweg).
Häufige Herausforderungen bei gewichteten Durchschnitten
Obwohl gewichtete Durchschnitte leistungsstarke Werkzeuge sind, bringen sie ihre eigenen potenziellen Fallstricke mit, die Sie sorgfältig umschiffen sollten.
Gewichtsauswahl
Die kritischste Herausforderung liegt in der Wahl geeigneter Gewichte, die Domänenexpertise und sorgfältige Überlegung darüber erfordert, was jeder Datenpunkt repräsentiert. Eine schlechte Gewichtsauswahl kann Ergebnisse dramatisch verzerren und zu irreführenden Schlussfolgerungen führen.
Wenn Sie beispielsweise Kundenzufriedenheitswerte berechnen und versehentlich weniger zuverlässigen Datenquellen höhere Gewichte zuweisen, wird Ihr endgültiger Durchschnitt die wahre Kundenzufriedenheit nicht genau widerspiegeln. Stellen Sie immer sicher, dass Ihre Gewichte die tatsächliche Bedeutung oder Zuverlässigkeit jedes Datenpunkts widerspiegeln.
Rechnerische Fallstricke
Neben der Gewichtsauswahl gehören zu häufigen Rechenfehlern die Verwendung von Nullgewichten (die Datenpunkte entfernen), negativen Gewichten (die kontraintuitive Ergebnisse produzieren können) und das Vergessen der notwendigen Normalisierung von Gewichten. Eine Division durch Null tritt auf, wenn alle Gewichte Null sind.
Überprüfen Sie immer Ihre Gewichtszuweisungen und stellen Sie eine korrekte Normalisierung sicher, insbesondere wenn Sie mit prozentbasierten Gewichten arbeiten, die zu 100 % summieren sollten.
So berechnen Sie den gewichteten Durchschnitt: Excel, KI und Python
Nachdem wir die Theorie und potenziellen Herausforderungen behandelt haben, wenden wir uns der praktischen Seite zu. Die Berechnung eines gewichteten Durchschnitts kann auf mehrere Arten erfolgen, von traditionellen Formeln bis hin zu modernen KI-gestützten Tools.
Methode 1: Die traditionelle Excel-Methode (mit Formeln)
Excel macht die Berechnung gewichteter Durchschnitte mit den Funktionen SUMPRODUCT() und SUM() unkompliziert. SUMPRODUCT multipliziert entsprechende Komponenten in den gegebenen Arrays und gibt die Summe dieser Produkte zurück.
Die Formelstruktur ist:
=SUMPRODUCT(values, weights)/SUM(weights)
Wenn sich Ihre Werte beispielsweise in den Zellen A2:A6 und ihre entsprechenden Gewichte in B2:B6 befinden, lautet die Formel:
=SUMPRODUCT(A2:A6, B2:B6) / SUM(B2:B6)
Diese Methode ist zuverlässig, erfordert jedoch, dass Sie die richtigen Funktionen kennen und sicherstellen, dass Ihre Zellbereiche korrekt sind. Für große oder dynamische Datensätze kann die Verwaltung dieser Formeln umständlich werden.
Methode 2: Die moderne KI-Methode (mit Excelmatic)
Ein schnellerer und intuitiverer Ansatz ist die Verwendung eines KI-Excel-Agenten wie Excelmatic. Anstatt Formeln zu schreiben, können Sie Ihre Anfrage einfach in natürlicher Sprache stellen. Excelmatic übernimmt den Rest, von der Interpretation Ihrer Anfrage bis zur Durchführung der Berechnung.
So funktioniert es:
- Laden Sie Ihre Excel-Datei hoch, die die Werte und Gewichte enthält.
- Stellen Sie Ihre Frage in natürlicher Sprache.
Für das gleiche Beispiel würden Sie einfach fragen:
Berechne den gewichteten Durchschnitt der Werte in Spalte A unter Verwendung der Gewichte in Spalte B.
Excelmatic verarbeitet Ihre Daten sofort und liefert die Antwort, sodass Sie sich keine Formeln merken oder sich um Zellbezüge sorgen müssen.
Vergleich: Traditionelle Formel vs. KI-Agent
| Merkmal | Traditionelles Excel (SUMPRODUCT) | KI-gestütztes Excelmatic |
|---|---|---|
| Aufwand | Erfordert Kenntnis der Funktionen SUMPRODUCT und SUM sowie korrekter Syntax. |
Einfach in natürlicher Sprache fragen. Keine Formeln nötig. |
| Geschwindigkeit | Schnell für erfahrene Benutzer, aber anfällig für Tippfehler und Bereichsfehler. | Sofort. Die KI übernimmt alle Backend-Berechnungen. |
| Flexibilität | Starr. Die Formel muss manuell aktualisiert werden, wenn sich Datenbereiche ändern. | Hochflexibel. Die KI versteht Kontext und passt sich neuen Fragen an. |
| Lernkurve | Mittel. Sie müssen spezifische Excel-Funktionen lernen und merken. | Praktisch null. Wenn Sie eine Frage stellen können, können Sie es verwenden. |
Die Verwendung eines KI-Tools wie Excelmatic vereinfacht nicht nur den Prozess, sondern reduziert auch die Fehleranfälligkeit, was Ihre Analyse schneller und genauer macht.
Methode 3: So berechnen Sie den gewichteten Durchschnitt in Python
Für diejenigen, die mit Python arbeiten, bietet die NumPy-Bibliothek eine elegante Lösung, obwohl Sie gewichtete Durchschnitte auch manuell berechnen können:
import numpy as np
# Werte und Gewichte definieren
values = [85, 92, 78, 95]
weights = [0.2, 0.3, 0.25, 0.25]
# Gewichteten Durchschnitt berechnen
weighted_avg = np.average(values, weights=weights)
print(f"Weighted average: {weighted_avg:.2f}")
# Alternative manuelle Berechnung
manual_calc = sum(v * w for v, w in zip(values, weights)) / sum(weights)
print(f"Manual calculation: {manual_calc:.2f}")
Die Formel für den gewichteten Durchschnitt in echten, domänenspezifischen Anwendungen
Nachdem Sie nun wissen, wie man gewichtete Durchschnitte berechnet, erkunden wir, wie sie reale Probleme in verschiedenen Bereichen lösen. Diese Beispiele helfen Ihnen, Situationen zu erkennen, in denen gewichtete Durchschnitte Ihre eigene Analyse verbessern können.
Akademisches Benotungssystem
Akademische Benotungssysteme verwenden häufig gewichtete Durchschnitte, um verschiedene Arten von Leistungsnachweisen auszugleichen. Ein typischer Kurs könnte Prüfungen mit 60 %, Hausaufgaben mit 25 % und Teilnahme mit 15 % gewichten.
Wenn ein Schüler 88 in Prüfungen, 95 in Hausaufgaben und 92 in Teilnahme erreicht, wäre seine Endnote: (88×0,6) + (95×0,25) + (92×0,15) = 90,35. Dieser Ansatz stellt sicher, dass wichtigere Leistungsnachweise einen größeren Einfluss auf die Endnote haben.
Finanzielle Lagerbewertung
In Geschäftsanwendungen verwenden Unternehmen häufig die gewichtete Durchschnittskostenmethode (Weighted Average Cost, WAC), um Lagerbestände zu bewerten, wenn Waren in einem Zeitraum zu unterschiedlichen Preisen gekauft werden. Im Gegensatz zu einem einfachen arithmetischen Mittel bezieht WAC die Einkaufsmengen ein, was Preisschwankungen glättet und eine konsistente Kostenbasis für die Finanzberichterstattung bietet.
Wenn ein Unternehmen beispielsweise 100 Einheiten zu 10 € und 300 Einheiten zu 12 € kauft, betragen die gewichteten Durchschnittskosten 11,50 €, nicht 11,00 €, wie ein einfacher Durchschnitt nahelegen würde.
Finanzanalyse
In der Finanzwelt gehen gewichtete Durchschnitte weit über das Lager hinaus. Das Portfoliomanagement stützt sich auf sie, um erwartete Renditen und Risiken zu berechnen, wobei das Gewicht jedes Vermögenswerts auf seinem Anteil am Gesamtwert des Portfolios basiert. Dies stellt sicher, dass größere Positionen mehr Einfluss haben als kleinere.
Ebenso wendet der Weighted Average Cost of Capital (WACC) das gleiche Prinzip an: Er repräsentiert die durchschnittlichen Finanzierungskosten eines Unternehmens, indem er die Kosten für Fremd- und Eigenkapital proportional zu ihrem Anteil an der Kapitalstruktur gewichtet. WACC ist eine wichtige Eingangsgröße in Bewertungsmodellen und Investitionsentscheidungen, da er als Hürdenrate des Unternehmens für die Erzielung von Renditen dient.
Statistische Umfragen
In der Forschungswelt verwendet die Umfrageanalyse gewichtete Durchschnitte, um demografische Ungleichgewichte auszugleichen und repräsentative Ergebnisse sicherzustellen. Wenn Ihre Umfrage bestimmte Altersgruppen unterrepräsentiert, können Sie Antworten gewichten, um der tatsächlichen Bevölkerungsverteilung zu entsprechen.
Diese Anpassung hilft, Stichprobenverzerrungen zu eliminieren und genauere Einblicke in die breitere Bevölkerung zu liefern, die Sie untersuchen.
Lagerbuchhaltung
Zurück zu praktischen Geschäftsanwendungen: Die gleitende Durchschnittsmethode in der Lagerbuchhaltung verwendet gewichtete Durchschnitte, um die Herstellungskosten zu bestimmen. Jeder neue Einkauf aktualisiert die durchschnittlichen Kosten pro Einheit basierend auf dem verbleibenden Lagerbestand und neuen Zugängen.
Dieser Ansatz glättet Preisschwankungen und liefert stabile Kostenschätzungen für die Finanzberichterstattung, was es einfacher macht, Rentabilitätstrends über die Zeit zu verfolgen.
Flächengewichtete Gebäudeeingaben und andere spezialisierte Kontexte
Über diese häufigen Anwendungen hinaus verwenden Ingenieuranwendungen oft flächengewichtete Durchschnitte für Gebäudeenergieberechnungen, bei denen verschiedene Zonen basierend auf ihrer Größe zur Gesamtleistung des Gebäudes beitragen.
Ähnliche Konzepte erscheinen in Geoinformationssystemen (GIS) für räumliche Analysen und in der Fertigung für die Qualitätskontrolle über verschiedene Produktionsbereiche hinweg.
Vergleichsanalyse mit anderen Durchschnittsarten
Mit all diesen Anwendungen im Hinterkopf fragen Sie sich vielleicht, wie Sie zwischen gewichteten Durchschnitten und anderen Durchschnittsmethoden wählen sollen. Das Verständnis dieser Unterscheidungen hilft Ihnen, den richtigen Ansatz für Ihre spezifische Situation auszuwählen.
Arithmetisches vs. gewichtetes Mittel
Arithmetische Mittel gehen davon aus, dass alle Datenpunkte gleich wichtig und repräsentativ sind. Gewichtete Durchschnitte berücksichtigen explizit Unterschiede in Wichtigkeit, Zuverlässigkeit oder Häufigkeit zwischen Datenpunkten.
Wählen Sie gewichtete Durchschnitte, wenn Ihre Daten natürlicherweise unterschiedliche Bedeutungsebenen haben oder wenn Sie Stichprobenungleichgewichte ausgleichen müssen. Verwenden Sie einfache arithmetische Mittel, wenn alle Datenpunkte wirklich gleiche Berücksichtigung verdienen.
Geometrisches Mittel
Geometrische Mittel eignen sich am besten für multiplikative Daten wie Wachstumsraten oder Verhältnisse, bei denen Sie die durchschnittliche Veränderungsrate über die Zeit ermitteln möchten. Geometrische Mittel lassen jedoch keine natürliche Gewichtung zu.
Während Sie gewichtete geometrische Mittel mit






