現代 Excel 標準差計算指南

標準差告訴我們數據集中數值的離散程度。許多重要的統計概念和方法，如變異數、變異係數和信賴區間，都依賴標準差作為衡量變異性的基礎指標，這使其成為數據專業人士必須掌握的最重要統計工具之一。

本文將向您介紹標準差，引導您使用傳統的公式和現代的AI工具在 Excel 中計算它，解釋可用方法之間的差異，並演示如何解讀結果以根據您的分析做出明智決策。

在 Excel 中計算標準差的兩種方法

談到計算標準差，您在 Excel 中有兩條主要途徑：現代化的對話式 AI 方法和傳統的基於公式的方法。

AI 驅動的方式：使用 Excelmatic

最快、最直觀的方法是使用像 Excelmatic 這樣的 AI 助手。您無需記憶函數和語法，只需用簡單的語言提出需求即可。

使用 Excelmatic 的過程很簡單：

1. 上傳包含數據集的 Excel 檔案。
2. 直接提問，例如：
   • "計算 B 欄每日銷售額的標準差。"
   • "我的銷售數據的樣本標準差是多少？"
   • "顯示每日銷售額的變異性。"

Excelmatic 會處理其餘一切。它會自動識別數據，套用正確的統計公式（母體或樣本），並立即提供答案。這種方法消除了記憶 STDEV.P 和 STDEV.S 之間差異或擔心儲存格範圍的需要，為您節省時間並減少出錯的機會。

傳統公式方式：使用 Excel 函數

要在 Excel 中手動計算標準差，您可以使用 STDEV.P() 函數計算母體標準差，或使用 STDEV.S() 函數計算樣本標準差。

例如，如果您的數據位於儲存格 B2 到 B31，您可以輸入 =STDEV.P(B2:B31) 來計算母體標準差，或輸入 =STDEV.S(B2:B31) 來計算樣本標準差。然後 Excel 將計算並顯示結果。雖然有效，但此方法需要您知道哪個函數適合您的數據。

什麼是標準差？

標準差是一種統計量度，用於量化一組數值中的變異或離散程度。它表示數據集中的值偏離數據集平均值（平均數）的程度。

它有助於理解數據內的變異性範圍——低標準差表示值接近平均值，暗示一致性；而高標準差表示更大的變異性，暗示數據更為分散。

標準差公式

標準差的公式取決於我們處理的是母體還是樣本。母體標準差 (σ) 的公式如下：

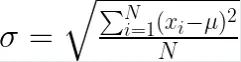
其中：

• N 是母體中的數據點總數。
• x_i​ 代表每個單獨的數據點。
• μ 是母體的平均值。

此公式計算與平均值偏差的平方的平均值，然後取該平均值的平方根。

樣本標準差 (s) 的公式如下。請注意，對於樣本標準差，我們按照慣例使用小寫的 n。

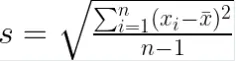
其中：

• n 是樣本中的數據點總數。
• x_i​ 代表每個單獨的數據點。
• xˉ 是樣本的平均值。

該公式與母體標準差的公式相似，但在分母中使用 n - 1（貝塞爾校正）來考慮樣本是用於估計母體參數這一事實。這種校正使樣本標準差成為母體標準差的無偏估計量。​​

標準差的實際應用

標準差是跨領域常用的技術。它為數據變異性和一致性提供了有價值的洞察，可應用於多個領域，包括：

• 風險評估： 標準差可以衡量資產回報的波動性。較高的標準差表示更大的風險和潛在回報變異性。
• 品質控制： 製造業使用標準差來監控和控製產品品質，確保一致性和符合標準。
• 醫療保健與醫學： 標準差用於理解如患者血壓或膽固醇水平等數據的分布，有助於識別異常值和正常範圍。
• 教育與研究： 標準差有助於確定考試分數的分布並評估教育干預措施的有效性。
• 天氣與氣候研究： 氣象學家使用標準差來分析天氣數據，例如溫度和降水量，以了解氣候變異性。

Excel 中的標準差函數類型

Microsoft Excel 有兩種不同的函數來計算標準差，具體取決於您處理的是整個母體還是樣本。

STDEV.P() 用於母體標準差

Excel 中的 STDEV.P() 函數計算整個母體的標準差。此函數假設提供的參數包含整個母體。STDEV.P() 函數的語法如下：

STDEV.P(number1, [number2], ...)

參數為：

• number1：第一個數字參數，對應於一個母體。
• [number2], ...：可選的附加數字或引用，對應於一個母體，最多 254 個參數。

當您的數據代表感興趣的整個母體時，應使用 STDEV.P()，例如，某所學校所有學生的考試分數。

STDEV.S() 用於樣本標準差

Excel 中的 STDEV.S() 函數計算母體樣本的標準差。此函數假設提供的參數是母體的樣本，而非整個母體。STDEV.S() 函數的語法如下：

STDEV.S(number1, [number2], ...)

參數為：

• number1：第一個數字參數，對應於母體的一個樣本。
• [number2], ...：可選的附加數字或引用，對應於一個樣本，最多 254 個參數。

在實踐中，當我們擁有樣本數據時，我們使用 STDEV.S() 來估計整個母體的標準差。例如，如果您正在分析從一所學校隨機選取的部分學生的考試分數，STDEV.S() 是合適的選擇。

計算標準差：一個實際範例

想像您是一名數據分析師，負責分析一家小型零售店的銷售表現。店主希望了解過去一個月每日銷售額的變異性，以便更好地管理庫存和人員配置。

您已收集了 30 天的每日銷售數據。讓我們將這些記錄放在 Excel 試算表的某一欄中，例如 B2 到 B31。

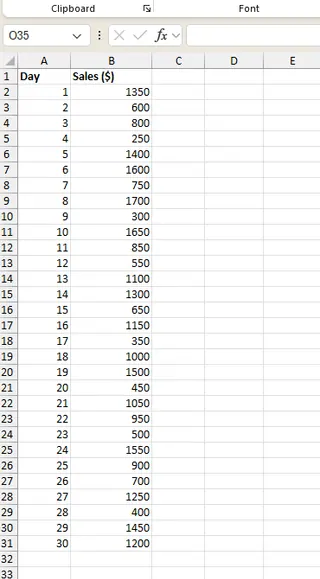
讓我們比較兩種方法來找出標準差。

方法 1：傳統公式法

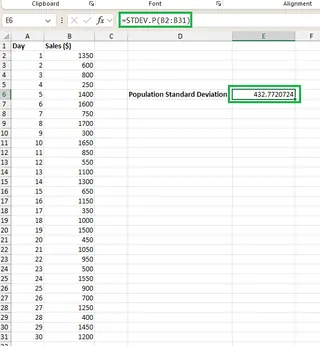
由於我們的分析涵蓋了整個月的銷售數據（我們感興趣的完整母體），我們使用 STDEV.P() 函數。在儲存格 E6 中，輸入以下公式：

=STDEV.P(B2:B31)

Excel 計算出母體標準差。

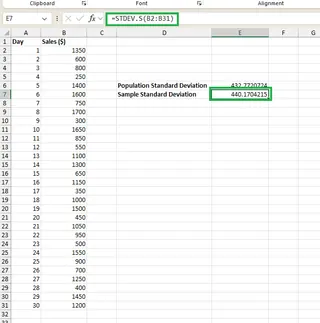
現在，假設我們將這 30 天的數據作為一個樣本來估計全年的表現。我們將改用 STDEV.S() 函數：

=STDEV.S(B2:B31)

這將給出樣本標準差。

方法 2：Excelmatic AI 方法

使用 Excelmatic，您只需上傳試算表並提問：

計算 B2:B31 數據的母體標準差。

或者，如果您將其視為樣本：

每日銷售額的樣本標準差是多少？

Excelmatic 會立即提供答案，無需您選擇函數或輸入公式。當您不確定該使用哪個公式時，這尤其有用，因為您可以描述您的目標，AI 將處理統計細節。

解讀標準差值

計算出標準差後，下一步是解讀結果。為了有效地做到這一點，了解數據的平均值也很有幫助。

您可以在 Excel 中使用 =AVERAGE(B2:B31) 計算平均值，或者詢問 Excelmatic："每日銷售額的平均值是多少？"。

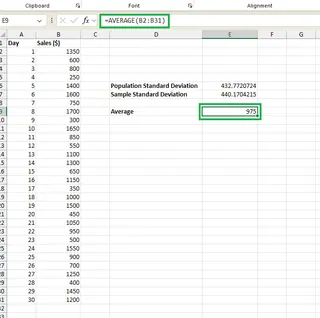
平均值為 $975，我們可以解讀標準差值：

• 母體標準差 (~$432.77)： 這表示，平均而言，每日銷售額與 $975 的平均值相差約 $432.77。這個數字代表了這個特定月份銷售數據的離散程度。
• 樣本標準差 (~$440.17)： 這個值略高。如果我們將這 30 天作為樣本來估計更長時期（例如全年）的變異性，這個值是相關的。較高的值考慮了使用樣本的不確定性。
• 銷售額的高變異性： 兩個值都表明變異性很高。銷售額與平均值相比波動很大，這可能會影響庫存和人員配置。這種不一致性表明可能需要進一步分析以更準確地預測每日銷售額。

店主在規劃時應考慮這種變異性，以避免在銷售清淡的日子庫存過多，或在繁忙的日子人手不足。

如何在 Excel 中添加標準差誤差線

視覺化變異性非常有效。在 Excel 圖表中添加標準差誤差線是實現此目的的好方法。

AI 方式：Excelmatic

這是 AI 助手大顯身手的另一個領域。只需提問：

為每日銷售額創建一個帶有標準差誤差線的折線圖。

Excelmatic 將在一個步驟中為您生成完整的圖表。

傳統方式：在 Excel 中手動製圖

1. 選擇您的數據範圍（B2 到 B31）。
2. 轉到 插入 選項卡並選擇圖表類型（例如，折線圖）。

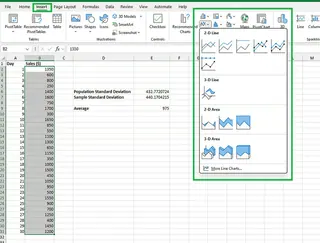
您將得到一個簡單的折線圖。

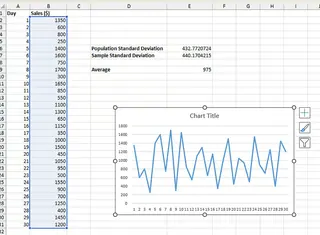
3. 點擊圖表以顯示 圖表設計 選項卡。
4. 點擊 添加圖表元素 > 誤差線 > 標準差。

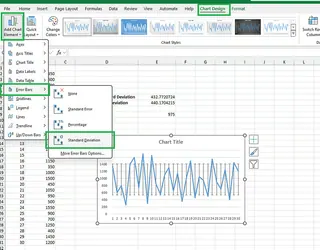
5. 要自定義，您可以選擇 更多誤差線選項... 來調整外觀。

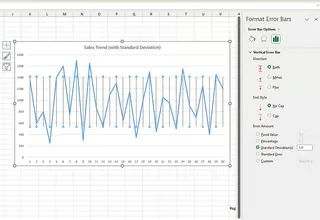
比較這兩種方法，AI 方法顯然更快，且無需在選單中導航。

結論

掌握標準差是進行穩健數據分析的基礎，它為變異性提供了關鍵洞察。本指南展示了 Excel 內的兩種不同方法：內建函數（STDEV.P、STDEV.S）的基礎精確性和 AI 驅動工具的現代效率。

從手動輸入公式到對話式 AI 的演進，正如 Excelmatic 所體現的，代表了數據工作流程的重大轉變。這種轉變將焦點從計算的技術性如何轉移到解讀的戰略性為何。通過將複雜的統計語法抽象為簡單的語言指令，AI 使專業人士能夠以更高的速度、準確性和信心執行複雜的分析。最終優勢不僅在於更快地獲得結果，還在於釋放認知資源，用於更高價值的任務，如洞察生成和戰略決策制定。

👉 體驗使用簡單語言指令分析 Excel 數據。立即免費開始使用 Excelmatic。

常見問題

在 Excel 中，何時應使用 STDEV.S() 函數而非 STDEV.P() 函數？

當您處理的是母體的樣本而非整個母體時，應使用 STDEV.S() 函數。當您的數據代表整個母體時，請使用 STDEV.P() 函數。

如何解讀數據集中的低標準差？

低標準差表示數據集中的值接近平均值，這意味著數據點與平均值持續相似。這暗示數據的變異性低、可靠性高，與平均值的偏差較少。

為什麼標準差在評估回歸模型的準確性時很重要？

標準差在評估回歸模型的準確性時很重要，因為它量化了殘差（模型預測中的誤差）的離散程度。通過計算殘差的標準差，分析師可以評估回歸模型對數據的擬合程度。

數據集的高標準差表明什麼？

高標準差表明數據集中的值分布在更廣的範圍內。這意味著存在更大的變異性或與平均值的離散程度，暗示數據不一致，值與平均值存在顯著偏差。

Excel 中 STDEV.P() 和 STDEV.S() 有什麼區別？

STDEV.P() 和 STDEV.S() 的主要區別在於它們的應用和計算方式。STDEV.P() 用於整個母體，除以數據點總數 (N)。而 STDEV.S() 用於母體樣本，除以數據點數減一 (n-1) 以考慮樣本變異性，這也稱為貝塞爾校正。