Excelで標準偏差を計算するための現代的なガイド

標準偏差は、特定のデータセット内の数値がどの程度広がっているかを示します。分散、変動係数、信頼区間など、いくつかの重要な統計概念や手法は、変動性の基本的な尺度として標準偏差に依存しており、データプロフェッショナルが習得すべき統計学における最も重要なツールの一つとなっています。

この記事では、標準偏差を紹介し、従来の数式と最新のAIツールの両方を使用してExcelで計算する方法を案内し、利用可能な方法の違いを説明し、分析に基づいて情報に基づいた意思決定を行うために結果を解釈する方法を実演します。

Excelで標準偏差を計算する2つの方法

標準偏差を計算する際、Excelには主に2つの方法があります：現代的な会話型AIアプローチと、従来の数式ベースの方法です。

AIを活用した方法：Excelmaticの使用

最も速く直感的に作業を完了する方法は、Excelmatic のようなAIエージェントを使用することです。関数や構文を覚える代わりに、平易な言語で必要なものを尋ねるだけです。

Excelmaticでは、プロセスはシンプルです：

1. データセットを含むExcelファイルをアップロードします。
2. 直接的な質問をします。例えば：
   • 「B列の日次売上の標準偏差を計算してください。」
   • 「私の売上データの標本標準偏差は何ですか？」
   • 「日次売上の変動性を見せてください。」

Excelmaticが残りのすべてを処理します。データを自動的に識別し、適切な統計式（母集団または標本）を適用し、即座に答えを提供します。このアプローチにより、STDEV.P と STDEV.S の違いを覚えたり、セル範囲を心配したりする必要がなくなり、時間を節約しエラーの可能性を減らします。

従来の数式による方法：Excel関数の使用

Excelで手動で標準偏差を計算するには、母集団の場合は STDEV.P() 関数を、標本の場合は STDEV.S() 関数を使用します。

例えば、データがセル B2 から B31 にある場合、母集団標準偏差を計算するには =STDEV.P(B2:B31) と入力し、標本標準偏差の場合は =STDEV.S(B2:B31) と入力します。Excelは計算を行い結果を表示します。この方法は効果的ですが、データに適した関数を知っている必要があります。

標準偏差とは？

標準偏差は、数値のセットにおける変動または分散の量を定量化する統計的尺度です。これは、データセット内の値がデータセットの平均からどの程度逸脱しているかを示します。

データ内の変動性の程度を理解するのに役立ちます。標準偏差が低いということは、値が平均に近く、一貫性があることを示唆します。一方、標準偏差が高いということは、変動性が大きく、データがより広がっていることを示唆します。

標準偏差の公式

標準偏差の公式は、母集団を扱っているか標本を扱っているかによって異なります。母集団標準偏差（σ）の公式は以下の通りです：

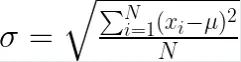
ここで：

• N は母集団内のデータポイントの総数です。
• x_i​ は個々のデータポイントを表します。
• μ は母集団の平均です。

この公式は、平均からの偏差の二乗の平均を計算し、その平均の平方根を取ります。

標本標準偏差（s）の公式は以下の通りです。標本標準偏差では、慣例として小文字の n を使用することに注意してください。

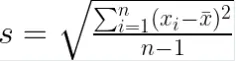
ここで：

• n は標本内のデータポイントの総数です。
• x_i​ は個々のデータポイントを表します。
• xˉ は標本の平均です。

この公式は母集団標準偏差のものと似ていますが、分母に n - 1（ベッセルの補正）を使用して、標本が母集団パラメータを推定するために使用されているという事実を考慮に入れています。この補正により、標本標準偏差は母集団標準偏差の不偏推定量となります。​​

標準偏差の実用的な応用

標準偏差は、分野を問わず一般的に使用される手法です。データの変動性と一貫性に関する貴重な洞察を提供し、以下の分野を含む様々な領域で応用できます：

• リスク評価： 標準偏差は資産収益の変動性を測定するために使用できます。標準偏差が高いほど、リスクと潜在的な収益の変動性が大きいことを示します。
• 品質管理： 製造業では、製品の品質を監視・管理し、一貫性と基準への適合を確保するために標準偏差を使用します。
• 医療・医学： 標準偏差は、患者の血圧やコレステロール値などのデータの広がりを理解し、外れ値や正常範囲を特定するために使用されます。
• 教育・研究： 標準偏差は、テストスコアの分布を決定し、教育的介入の効果を評価するのに役立ちます。
• 気象・気候研究： 気象学者は、気温や降水量などの気象データを分析し、気候変動性を理解するために標準偏差を使用します。

Excelにおける標準偏差関数の種類

Microsoft Excelには、母集団全体を扱っているか標本を扱っているかによって、標準偏差を計算する2つの異なる関数があります。

母集団標準偏差用の STDEV.P()

Excelの STDEV.P() 関数は、母集団全体の標準偏差を計算します。この関数は、提供された引数が母集団全体を含むと仮定します。STDEV.P() 関数の構文は以下の通りです：

STDEV.P(number1, [number2], ...)

パラメータは：

• number1: 母集団に対応する最初の数値引数。
• [number2], ...: オプションの追加の数値または母集団に対応する参照。最大254個の引数。

データが関心のある母集団全体を表す場合、例えば特定の学校の全生徒のテストスコアなど、STDEV.P() を使用すべきです。

標本標準偏差用の STDEV.S()

Excelの STDEV.S() 関数は、母集団の標本の標準偏差を計算します。この関数は、提供された引数が母集団全体ではなく、母集団の標本であると仮定します。STDEV.S() 関数の構文は以下の通りです：

STDEV.S(number1, [number2], ...)

パラメータは：

• number1: 母集団の標本に対応する最初の数値引数。
• [number2], ...: オプションの追加の数値または標本に対応する参照。最大254個の引数。

実際には、データの標本がある場合、母集団全体の標準偏差を推定するために STDEV.S() を使用します。例えば、学校から無作為に選ばれた生徒の一部のテストスコアを分析している場合、STDEV.S() が適切な選択です。

標準偏差の計算：実用的な例

あなたがデータアナリストで、小売店の販売実績を分析する任務を負っていると想像してください。オーナーは、在庫管理と人員配置をより適切に行うために、過去1か月間の日次売上の変動性を理解したいと考えています。

あなたは30日間の日次売上データを収集しました。これらの記録を、Excelスプレッドシートの B2 から B31 の列に入れましょう。

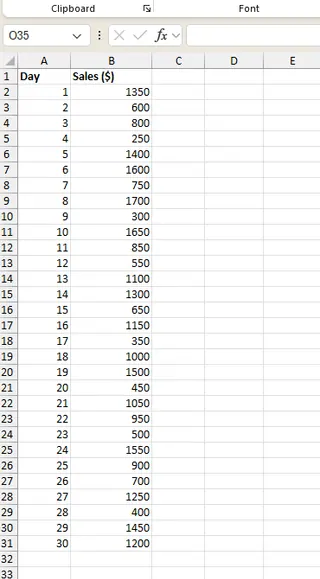
標準偏差を見つけるための2つの方法を比較してみましょう。

方法1：従来の数式アプローチ

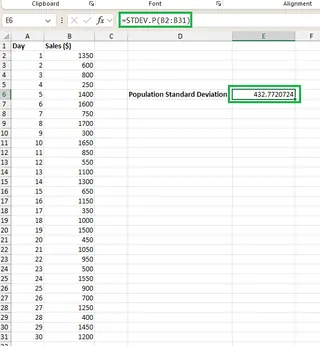
私たちの分析は1か月分の売上データ全体（関心のある完全な母集団）をカバーしているため、STDEV.P() 関数を使用します。セル E6 に、次の数式を入力します：

=STDEV.P(B2:B31)

Excelが母集団標準偏差を計算します。

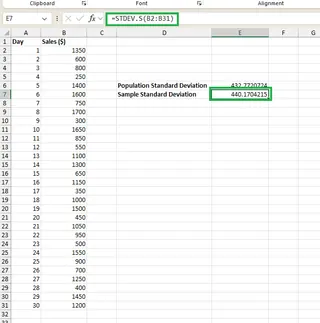
さて、この30日間のデータを1年間全体の実績を推定するための標本として使用していると仮定しましょう。その場合は、代わりに STDEV.S() 関数を使用します：

=STDEV.S(B2:B31)

これにより、標本標準偏差が得られます。

方法2：Excelmatic AIアプローチ

Excelmaticでは、スプレッドシートをアップロードして次のように尋ねるだけです：

B2:B31のデータの母集団標準偏差を計算してください。

または、標本として扱う場合は：

日次売上の標本標準偏差は何ですか？

Excelmaticは、関数を選択したり数式を入力したりする必要なく、即座に答えを提供します。これは、どの数式を使用すべきかわからない場合に特に便利です。目標を説明するだけで、AIが統計的な詳細を処理します。

標準偏差の値の解釈

標準偏差を計算した後、次のステップは結果を解釈することです。これを効果的に行うには、データの平均も知っておくと役立ちます。

これはExcelで =AVERAGE(B2:B31) を計算するか、Excelmaticに「日次売上の平均は何ですか？」と尋ねることで求めることができます。

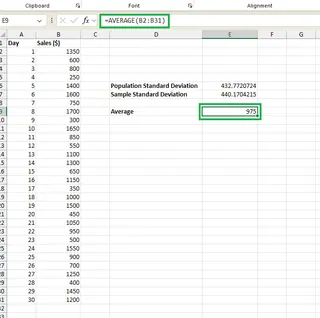
平均が $975 なので、標準偏差の値を解釈できます：

• 母集団標準偏差（約$432.77）： これは、日次売上が平均$975から平均して約$432.77変動することを示しています。この数字は、この特定の月の売上データの広がりを表しています。
• 標本標準偏差（約$440.17）： この値はわずかに高くなっています。この30日間をより長い期間（例えば1年間全体）の変動性を推定するための標本として扱う場合、これが関連する数字です。より高い値は、標本を使用することの不確実性を考慮に入れています。
• 売上の高い変動性： 両方の値は高い変動性を示しています。売上は平均から大きく変動しており、在庫や人員配置に影響を与える可能性があります。この一貫性のなさは、日次売上をより正確に予測するためにさらなる分析が必要かもしれないことを示唆しています。

店舗オーナーは、閑散期の過剰在庫や繁忙期の人員不足を避けるために計画を立てる際、この変動性を考慮すべきです。

Excelで標準偏差バーを追加する方法

変動性を視覚化することは強力です。Excelのチャートに標準偏差バーを追加するのは、これを行う優れた方法です。

AIによる方法：Excelmatic

これはAIエージェントが活躍するもう一つの領域です。次のように尋ねるだけです：

日次売上の折れ線グラフを標準偏差の誤差範囲付きで作成してください。

Excelmaticは、1ステップで完全なチャートを生成します。

従来の方法：Excelでの手動チャート作成

1. データ範囲（B2 から B31）を選択します。
2. 挿入 タブに移動し、チャートタイプ（例：折れ線グラフ）を選択します。

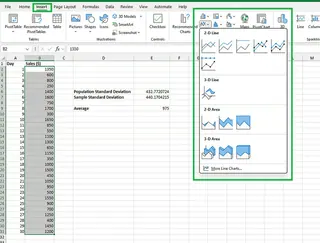
シンプルな折れ線グラフが得られます。

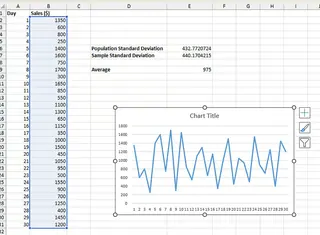
3. チャートをクリックして グラフのデザイン タブを表示します。
4. グラフ要素の追加 > 誤差範囲 > 標準偏差 をクリックします。

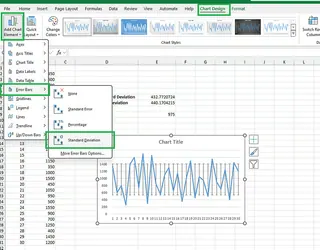
5. カスタマイズするには、その他の誤差範囲オプション... を選択して外観を調整できます。

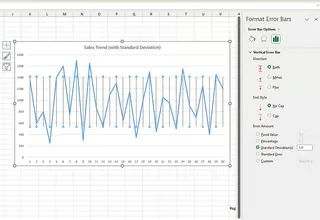
2つの方法を比較すると、AIアプローチの方が明らかに速く、メニューをナビゲートする必要がありません。

結論

標準偏差を習得することは、変動性に関する重要な洞察を提供する堅牢なデータ分析の基礎です。このガイドでは、Excel内での2つの異なるアプローチ、組み込み関数（STDEV.P、STDEV.S）の基礎的な精度と、AIを活用したツールの現代的な効率性を実証しました。

手動での数式入力から会話型AIへの進化は、Excelmaticに代表されるように、データワークフローにおける重要な変化を表しています。この移行は、計算の技術的な方法から解釈の戦略的な理由へと焦点を移します。複雑な統計構文をシンプルな言語コマンドに抽象化することで、AIは専門家がより高速に、正確に、自信を持って高度な分析を実行できるようにします。究極の利点は、結果をより速く得られることだけでなく、洞察の生成や戦略的意思決定のようなより付加価値の高いタスクに認知リソースを解放することにあります。

👉 シンプルな言語コマンドでExcelデータを分析する体験を。今すぐExcelmaticを無料で使い始める。

よくある質問

Excelでいつ STDEV.S() 関数の代わりに STDEV.P() 関数を使用すべきですか？

母集団全体ではなく、母集団の標本を扱っている場合に STDEV.S() 関数を使用すべきです。データが母集団全体を表す場合は、STDEV.P() 関数を使用してください。

データセットにおける低い標準偏差をどのように解釈しますか？

標準偏差が低いということは、データセット内の値が平均に近いことを示し、データポイントが平均値と一貫して類似していることを示唆します。これは、変動性が低くデータの信頼性が高く、平均からの逸脱が少ないことを意味します。

回帰モデルの精度を評価する際に、なぜ標準偏差が重要ですか？

標準偏差は、残差（モデルの予測誤差）の広がりを定量化するため、回帰モデルの精度を評価する上で重要です。残差の標準偏差を計算することで、アナリストは回帰モデルがデータにどの程度適合しているかを評価できます。

高い標準偏差はデータセットについて何を示していますか？

標準偏差が高いということは、データセット内の値がより広い範囲に広がっていることを示します。これは、変動性または平均からの分散が大きいことを意味し、データの一貫性がなく、値が平均から大きく逸脱していることを示唆します。

Excelにおける STDEV.P() と STDEV.S() の違いは何ですか？

STDEV.P()