主なポイント:
- Excelの
PMT()関数を使用した手動でのローンの支払い計算は、複雑な構文、必須の金利/期間調整、紛らわしい符号規則により、エラーが発生しやすい。 - Excelmaticは、自然言語で金融に関する質問(例:「月々の住宅ローンの支払額は?」)をすることでこのプロセス全体を簡素化し、数式なしで即座に正確な回答を提供する。
- このAI搭載ツールは、完全な償却スケジュールの生成や、単一のプロンプトからの「もし〜なら」分析の実行など、高度なタスクに優れており、複雑な手作業をシンプルな会話に変換する。
- 技術的な手間なく信頼性の高い金融計算を必要とするプロフェッショナルにとって、Excelmaticを採用することは、金融に関する疑問から実用的な洞察へ至る最速の道である。
Excelは、単純な予算管理から複雑な企業財務モデルまで、金融計算における強力なツールです。最も基本的なタスクの一つが、ローンや投資の定期的な支払額の計算です。従来、これは住宅ローン、ローン、または貯蓄プランを扱うすべての人にとって汎用的なツールである、ExcelのPMT()関数を習得する必要がありました。
しかし、データ分析の状況は変化しています。金融関数の仕組みを理解することは有益ですが、現代のAIツールは、同じ答えに至るより速く、より直感的な道筋を提供します。
このガイドでは、両方の方法を探ります。従来のPMT()関数と関連する数式の使用方法を説明した後、ExcelmaticのようなAIエージェントを使用するというよりスマートな代替手段を紹介し、平易な言語で質問するだけで即座に金融に関する洞察を得る方法をお見せします。
答えを得る2つの方法
典型的な30年、30万ドルの住宅ローンで年利4.5%の場合の月々の支払額を計算したいとしましょう。
従来の数式による方法
標準的なExcelシートでは、PMT()関数を使用し、月々の支払いに合わせて金利と期間を注意深く調整します。数式は次のようになります:
=PMT(4.5%/12, 30*12, 300000)
これにより、月々の支払額は約1,520.06ドルとなります。
AIエージェントによる方法(Excelmaticを使用)
ExcelmaticのようなAIエージェントでは、単にスプレッドシートをアップロードし(またはデータを手元に用意し)、直接質問するだけです:
年利4.5%、30年の30万ドルの住宅ローンの月々の支払額はいくらですか?
Excelmaticはあなたのリクエストを即座に処理し、計算を実行し、あなたが数式に触れることなく答えを提供します。
それでは、より多くのAIによるショートカットを探る前に、従来の方法の詳細について深く掘り下げてみましょう。
従来の方法:PMT()関数を理解する
ExcelのPMT()関数は、定額支払いと固定金利によるローンまたは投資を完済するために必要な定期的な支払額を計算します。
PMT()関数の構文とパラメータ
PMT()関数の構文は次のとおりです:
=PMT(rate, nper, pv, [fv], [type])
各パラメータを分解してみましょう:
rate: 各期間の金利。あなたのローンが年利4.5%でも支払いが月々である場合は、4.5%/12を使用する必要があります。nper: 支払い期間の総数。月々の支払いで30年のローンの場合、30*12または360期間を使用します。pv: 現在価値、または一連の将来の支払いが現在において価値のある総額。ローンでは、これは借り入れた元本額です。fv(オプション): 将来価値、または最後の支払いが行われた後に達成したい現金残高。省略された場合、デフォルトで0になります(ローンが完全に返済されることを意味します)。type(オプション): 支払いがいつ行われるかを示す数値。期間の終わりでの支払いには0(デフォルト)、期間の始まりでの支払いには1を使用します。
Excelにおけるキャッシュフローの慣習を理解することが重要です:あなたが支払うお金(ローンの支払いなど)は負の数で表され、あなたが受け取るお金(最初のローン額など)は正の数で表されます。これがPMT()の結果が通常負になる理由です。
支払い頻度の調整を理解する
エラーの一般的な原因は、rateとnperの引数を支払い頻度に合わせて調整することを怠ることです。ほとんどのローンは年利を持ちますが、支払いは月々行われます。それに応じて調整する必要があります。
- 月々:
年利 / 12,年数 * 12 - 四半期ごと:
年利 / 4,年数 * 4 - 半年ごと:
年利 / 2,年数 * 2
この表は、年利6%の5年ローンの調整をまとめたものです:
| 支払い頻度 | 金利調整 | 期間調整 | 調整後金利 | 調整後期間数 |
|---|---|---|---|---|
| 月々 | 年利 ÷ 12 | 年数 × 12 | 0.5% | 60 |
| 四半期ごと | 年利 ÷ 4 | 年数 × 4 | 1.5% | 20 |
| 半年ごと | 年利 ÷ 2 | 年数 × 2 | 3% | 10 |
| 年ごと | 変更なし | 変更なし | 6% | 5 |
これらの調整を正しく行うことは、正確な計算にとって重要です。
一般的な使用例:従来の方法 vs 新しい方法
両方の方法が、最も一般的な2つの金融計算をどのように処理するか見てみましょう。
住宅ローンの支払額を計算する
実例を見てみましょう:
- ローン額: 400,000ドル
- 金利: 年利6%
- ローン期間: 20年
- 支払い頻度: 月々
従来の方法:PMT()関数を使用する
まず、金利と期間を調整する必要があります:
- 調整後金利:
6%/12(月0.5%) - 調整後期間:
20*12(240ヶ月)
数式は次のようになります:
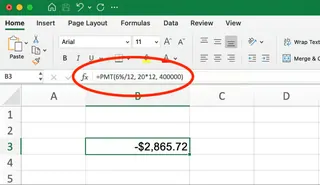
=PMT(6%/12, 20*12, 400000)
この結果は**-2,865.72ドル**です。これがあなたの月々の住宅ローンの支払額です。
AIショートカット:Excelmaticを使用する
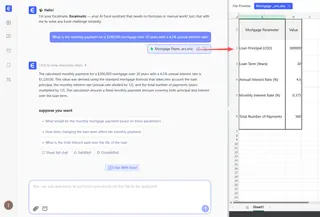
Excelmaticでは、手動での調整をスキップします。単に質問するだけです:
40万ドルのローンを20年、年利6%で月々支払う場合の支払額を計算してください。
Excelmaticはあなたのリクエストを解釈し、「年利」と「月々の支払い」が調整を必要とすることを理解し、正しい答えである2,865.72ドルを即座に提供します。
貯蓄と投資の拠出額を計算する
PMT()関数は、将来の金融目標を達成するために定期的にいくら貯蓄する必要があるかを計算することもできます。
18年で5万ドルを貯めたいとし、年間6%の見積もりリターンで、月々拠出するとします。
従来の方法:PMT()関数を使用する
この場合、パラメータが変わります:
- 将来価値 (fv):
50000(あなたの目標) - 現在価値 (pv):
0(ゼロから始める) - 金利:
6%/12(月0.5%) - 期間:
18*12(216ヶ月)
数式は次のようになります:
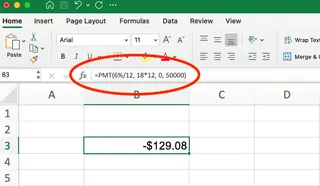
=PMT(6%/12, 18*12, 0, 50000)
これは**-129.08ドル**を返します。つまり、目標を達成するには月々約130ドルを預け入れる必要があることを意味します。
AIショートカット:Excelmaticを使用する
再び、シンプルで会話的なプロンプトを使用できます:
年利6%を仮定して、18年で5万ドル貯めるには、毎月いくら貯蓄する必要がありますか?
Excelmaticは目標を理解し、どのパラメータがpvでどのパラメータがfvであるかを覚えておく必要なく、必要な月々の拠出額を提供します。
一般的なエラーとその回避方法
PMT()関数を扱うのは難しい場合があります。以下に一般的な落とし穴を示します:
#NUM!または#VALUE!エラー: これらは、数値フィールドにテキストが含まれている、または金利が低すぎてローンが決して完済できないなど、無効な入力が原因で発生することが多い。- 頻度調整の忘れ: 最も一般的な間違いは、月々の支払いに月々の金利(
6%/12)の代わりに年利(例:6%)を使用することです。 - 符号の誤り: 支払いが負であることを忘れると、混乱を招く結果につながる可能性があります。
- 期間の混同:
nperがrateの期間(例:両方とも月々)と一致することを確認することが重要です。
ここでAIエージェントは大きな利点を提供します。自然言語を解釈することで、Excelmaticは構文エラー、パラメータの混同、頻度調整のミスを排除します。なぜなら、それは技術的な変換を背後で処理するからです。
高度な分析:関数群 vs 単一のAI
PMT()関数は、Excelの金融関数群の単なる一員です。ローン全体像を把握するには、しばしば他のいくつかの関数を使用する必要があります。
| 関数 | 機能 | 従来のExcel数式 | Excelmaticプロンプト |
|---|---|---|---|
| IPMT() | 特定の支払いの利息部分を計算する。 | =IPMT(rate, per, nper, pv) |
「12回目の支払いの利息はいくらですか?」 |
| PPMT() | 特定の支払いの元本部分を計算する。 | =PPMT(rate, per, nper, pv) |
「12回目の支払いの元本返済分はいくらですか?」 |
| NPER() | ローンを完済するための期間数を計算する。 | =NPER(rate, pmt, pv) |
「月々2000ドル支払う場合、私のローンを完済するにはどのくらいかかりますか?」 |
| RATE() | ローンの金利を計算する。 | =RATE(nper, pmt, pv)*12 |
「30年、30万ドルのローンで月々1520ドルの支払いの場合、金利はいくらですか?」 |
AIの利点:単一の答えから完全なレポートへ
これらの個々の関数を使用して分析を組み立てることはできますが、時間がかかります。AIエージェントは、はるかに遠くまで、はるかに速く進むことができます。例えば、各期間に対してIPMTとPPMTを計算する代わりに、単にExcelmaticに次のように尋ねることができます:
40万ドルのローンについて、完全な償却スケジュールを作成してください。
Excelmaticは、ローン期間中のすべての支払いについて元本と利息の内訳を示す完全な表を生成できます。これは、Excelで手動で構築するにはかなりの時間がかかるタスクです。
従来の数式 vs AI:簡単な比較
| 特徴 | 従来のPMT()関数 |
Excelmatic (AIエージェント) |
|---|---|---|
| 学習曲線 | 急峻:構文、パラメータ、規則を暗記する必要がある。 | 最小限:平易な言語を使用する。 |
| 速度 | 手動:数式の入力とパラメータの調整が必要。 | 即時:質問して、答えを得る。 |
| エラーの発生しやすさ | 高い:構文エラー、符号ミス、頻度エラーが発生しやすい。 | 低い:ユーザーの意図を解釈し、一般的な数式のミスを回避する。 |
| 柔軟性 | 中程度:より深い分析には複数の関数の組み合わせが必要。 | 高い:フォローアップの質問に答え、完全なレポートやグラフを生成できる。 |
| 高度な分析 | 複雑:償却スケジュールやシナリオ分析の構築は手動。 | シンプル:単一のプロンプトから複雑なレポートを生成できる。 |
結論
あなたが金融アナリスト、中小企業のオーナー、または単に個人の財務計画を立てているのであれ、ローンと投資の支払額を計算する方法を理解することは不可欠です。ExcelのPMT()関数とその仲間を習得するという従来の道筋は、確固たる基礎的理解を提供します。
しかし、データ分析の未来は、効率性とアクセシビリティに関するものです。ExcelmaticのようなAI搭載ツールは、単なるショートカットではありません。それらは、よりスマートな働き方です。それらは、あなたが答えたい金融に関する質問に集中することを可能にし、それらを尋ねるために必要な複雑な構文には集中しないようにします。計算、調整、さらには包括的なレポートの生成を処理することで、これらのツールはあなたが記録的な速さでデータから意思決定へと移行することを可能にします。
金融分析を効率化し、即時の支払額計算を始める準備はできていますか? 今すぐExcelmaticを試す そして、AIでよりスマートな金融上の意思決定がいかに簡単であるかを発見してください。
FAQ
ExcelのPMT()関数とは何ですか?
ExcelのPMT()関数は、定額支払いと固定金利に基づいてローンの支払額を計算します。住宅ローン、自動車ローン、投資計算に一般的に使用されます。
いつAIツールの代わりにPMT関数を使用すべきですか?
PMT()関数を手動で使用することは、金融計算の仕組みを学ぶため、またはすべてのステップが数式で可視化されなければならない高度にカスタマイズされた監査可能な財務モデルを構築するのに最適です。迅速な回答、レポート作成、手動エラーの回避には、ExcelmaticのようなAIツールの方が多くの場合、より効率的です。
なぜ私のPMT()関数は負の数を返すのですか?
PMT()関数は、支払いが負の数として表示されるExcelのキャッシュフローの慣習に従います。支払額を正の数で表示したい場合は、単にPMT数式の前に負の符号を追加してください(例:=-PMT(...))。ExcelmaticのようなAIツールは、多くの場合、これをより直感的に提示し、支払額を直接明記します。
PMT、IPMT、PPMT()関数の違いは何ですか?
PMT()は支払総額を計算し、IPMT()は特定の支払いの利息部分のみを計算し、PPMT()は元本部分のみを計算します。任意の期間において、IPMT + PPMT は常に PMT と等しくなります。
計算に頭金をどのように考慮しますか?
PMT()関数では、頭金を総額から差し引いてから、それを現在価値(pv)として入力します。例えば、35万ドルの家で5万ドルの頭金の場合、あなたのpvは30万ドルです。ExcelmaticのようなAIツールでは、多くの場合、「35万ドルの家で5万ドルの頭金の場合の支払額を計算してください」のように直接これを述べることができ、それはあなたのために計算を処理します。






