主なポイント:
- Excelで円の面積計算から複雑な三角関数まで、πを使用する場合、従来は
PI()のような数式を覚えて正確に入力する必要があり、非技術系ユーザーにとってはエラーの原因となり、時間もかかります。 - Excelmaticはこのプロセスを革新します。自然言語で計算内容を記述するだけで(例:「これらの円の面積を計算して」)、数式なしで瞬時に正確な結果を得られます。
- このAIを活用したアプローチは、複雑な手動数式が必要でエラーが発生しやすい高度なシナリオ、例えば複雑な方程式や単位変換を自動で処理する際に真価を発揮します。
- 数学的な頭痛を伴わずに正確な幾何学や三角関数の結果が必要なビジネスプロフェッショナルにとって、Excelmaticはデータ分析にπを取り入れる最速で最も信頼性の高い方法です。
Excelで円の面積を計算したり三角関数の公式を扱ったりする必要があったことがあれば、スプレッドシートにπ(パイ)をどうやって取り込むか考えたことがあるでしょう。手動で3.14159…と入力することもできますが、正確な結果に必要な精度がなく、手動エラーの原因となります。
従来の解決策は、Excelの組み込み関数PI()を使用することです。これは数十年にわたりユーザーを支えてきた信頼性の高い方法です。しかし、数式を一切覚える必要がなく、より速く、より直感的な方法があったらどうでしょうか?
この記事では、両方の方法を説明します。まず、従来のPI()関数について復習します。その後、Excelmaticを使用した現代的なAI活用アプローチを紹介し、単に質問するだけで同じ、あるいはさらに複雑な結果を得る方法をお見せします。
従来の方法: ExcelのPI()関数を理解する
PI()関数は、数学定数π(約3.14159)の値を返すExcelの組み込みの方法です。円や球体の計算に基本的なπですが、後述の例で見るように、多くの予期せぬ場面で登場します。
PI()関数は何をするのか?
PI()と単にセルに3.14と入力することの違いは何か疑問に思うかもしれません。答えは精度です。PI()を使用すると、Excelはπを15桁の有効数字(3.141592653589793)で返します。これは、ほとんどの計算に十分すぎる精度です。精度の低いハードコードされた数値を使用すると、特に科学技術計算において不正確さの原因となります。
PI()関数の構文
構文は可能な限りシンプルです:
=PI()
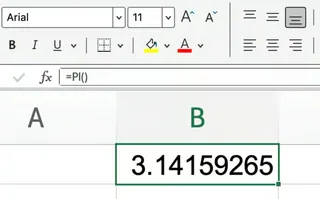
引数や調整するオプションはありません。括弧内に何か引数を入力しようとすると、Excelはエラーを返します。
数式でπを適用する: 手動の方法 vs AIの方法
PI()が何かを理解したところで、実際に使用してみましょう。以下では、従来のExcel数式を使用する方法と、ExcelmaticのようなAIエージェントを使用する方法を比較して、一般的な問題を解決する方法を見ていきます。
円の面積を計算する
半径から円の面積を計算する公式は、面積 = π × r² です。
従来の方法:
円の半径がセルA2にある場合、次の数式を入力します:
=PI() * (A2^2)

これはπに半径の2乗を掛け、面積を求めます。半径のリストがある場合は、この数式を列の下にドラッグします。
Excelmaticの方法:
数式は忘れてください。スプレッドシートをExcelmaticにアップロードし、平易な言葉で尋ねるだけです:
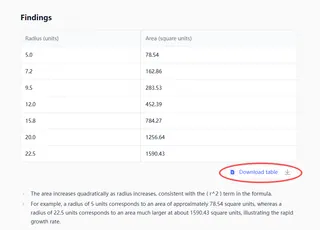
列Aにリストされている各半径について、円の面積を計算してください。
Excelmaticはあなたの要求を理解し、完全な精度で計算を実行し、新しい列に結果を返します。覚えるべき数式も、セルをドラッグする必要もありません。
円周を求める
円周は、公式 2 × π × r で求められます。
従来の方法:
半径がセルA2にある場合、Excelの数式は次の通りです:
=2 * PI() * A2
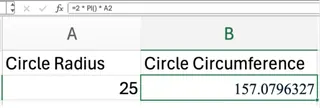
Excelmaticの方法:
再び、目標を述べるだけです:
列Aの半径を使用して、円の円周を求めてください。
Excelmaticは要求を処理し、瞬時に答えを提供します。
度をラジアンに変換する
ExcelのSIN()やCOS()などの三角関数は、度ではなくラジアンを使用します。度をラジアンに変換する公式は、度 × π / 180 です。
従来の方法:
度の値がA2にある場合、数式は次の通りです:
=A2 * PI() / 180
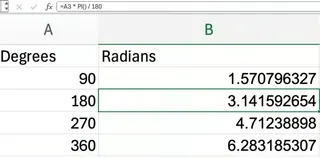
Excelmaticの方法:
プロセスを簡素化し、直接尋ねます:
列Aの角度を度からラジアンに変換してください。
これは覚えやすいだけでなく、手動で変換式を入力するよりもエラーが発生しにくくなります。
円柱の体積を計算する
円柱の体積は π × r² × h です。これには半径 (r) と高さ (h) の2つの変数が必要です。
従来の方法:
半径がセルA2、高さがB2にある場合、次の数式を使用します:
=PI() * (A2^2) * B2

Excelmaticの方法:
データと必要なことを説明するだけです:
列Aの半径と列Bの高さを使用して、円柱の体積を計算してください。
Excelmaticは列を変数に正しくマッピングし、データセット全体の体積を計算します。
AIの真の力: 複雑な数式の処理
数式が複雑になると、AIアプローチの利点は明らかになります。PI()は、記述が難しく、デバッグがさらに難しい高度な科学、工学、金融の方程式によく登場します。
球面三角法の余弦定理を考えてみましょう。これは球体(地球など)上の2点間の最短距離を計算します。
従来の方法:
デンバー(緯度/経度がB2/C2)とエディンバラ(緯度/経度がB3/C3)の間の距離を計算するには、この巨大な数式を記述する必要があります:
=3958*ACOS(SIN(B2*PI()/180)*SIN(B3*PI()/180)+COS(B2*PI()/180)*COS(B3*PI()/180)*COS((C3-C2)*PI()/180))
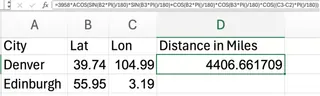
括弧の位置が1つ間違っていたり、セル参照が間違っていたりすると、数式全体が壊れます。強力ですが、非常に壊れやすいのです。結果の4,400.4マイルは、Googleの公式距離4,405マイルに非常に近い値です。
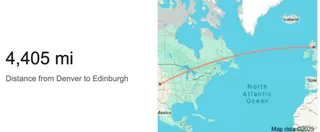
原著者が指摘しているように、この式でπに切り捨てた値(3.14など)を使用すると、精度の低い結果4,418.3マイルが得られます。精度が鍵です。
Excelmaticの方法:
その数式と格闘する代わりに、Excelmaticに目的を伝えるだけです:
私のファイルは、列Bに緯度、列Cに経度があります。デンバー(2行目)とエディンバラ(3行目)の間の距離をマイルで計算してください。
Excelmaticは複雑な三角法、度からラジアンへの変換、最終的な計算をバックグラウンドで処理します。頭を悩ませることなく正確な答えが得られ、時間を節約し、数式エラーのリスクを排除できます。
結論: 仕事に合った適切なツールを選ぶ
ExcelのPI()関数をマスターすることは、数学的公式を定期的に扱うすべての人にとって貴重なスキルです。これにより、計算が正確でプロフェッショナルなものになります。
しかし、データ分析の状況は変化しています。単純な一回限りの計算には、簡単な数式で十分かもしれません。しかし、複雑なタスク、繰り返しの計算、数式エラーが許されない状況では、ExcelmaticのようなAIエージェントが明確な利点を提供します。これにより、方法(数式の複雑な構文)ではなく、目的(ビジネス目標)に集中することができます。
今日、高度なExcelユーザーになるということは、従来の方法を知り、いつスマートなツールを活用して問題を解決し、プロセスを自動化し、他の人が見逃すかもしれない洞察を見つけるかを知ることを意味します。
πやその他の複雑な数式を複雑さなしに計算する準備はできていますか?今すぐExcelmaticを試して、数秒で数学的な質問に対する正確な答えを得ましょう。
よくある質問
PI()を他のExcel関数と一緒に使えますか?
はい、もちろんです。SIN()、COS()、SQRT()などの関数、または基本的な算術演算と組み合わせて、より複雑な数式を構築できます。
ExcelでPI()は小数点以下何桁まで返しますか?
PI()はπを15桁の有効数字で返します: 3.14159265358979。
PI(2)のように、PI()の中に値を入力するとどうなりますか?
Excelは#VALUE!エラーを返します。この関数は常にPI()と記述し、括弧内には何も入れないようにする必要があります。
πを少数点以下の桁数を減らして表示する簡単な方法はありますか?
Excelのセル書式設定オプションを使用して小数点以下の桁数を制限してください。数式内の基礎となる値は正確なまま保持されます。






