ExcelのNORM.DIST関数ガイド - 数式とAIの比較

Excelで確率や統計を扱うことが多いなら、品質管理の実施、テストスコアの評価、ビジネスデータの分析など、正規分布を分析する必要に必ず直面します。従来、これは特定の値に関連する確率を求めるためにNORM.DIST()のような関数を習得することを意味していました。

しかし今日、仕事を成し遂げる方法は複数あります。古典的な数式ベースのアプローチは精度と制御性を提供しますが、現代のAIツールは同じ答えに至る、より速く、より直感的な道筋を提供します。

このガイドでは、両方の方法を探求します。従来のNORM.DIST()関数、その構文、オプションを分解して説明します。その後、強力なAI駆動の代替手段であるExcelmaticを紹介し、質問するだけで同じ結果を得る方法をお見せします。最後まで読めば、Excelで正規分布分析を扱う方法の全体像を把握し、あなたのワークフローに最適な方法を選択できるようになるでしょう。

正規分布計算とは？

「方法」の前に、「何であるか」を明確にしましょう。正規分布計算は、釣鐘型のデータセットから抽出された値が特定の数値以下である確率を求めるのに役立ちます。ニーズに応じて、累積確率（ある点までの曲線下面積）または確率密度（その特定の点における曲線の高さ）のいずれかを得ることができます。

したがって、特定の数値以下をスコアする可能性がどれくらいあるかを知りたい場合、または単にある点での正規曲線の値が必要な場合、従来の方法とAIの方法の両方が対応しています。

方法 1: NORM.DIST()を使った従来の数式アプローチ

Excelの数式に慣れているユーザーにとって、NORM.DIST()はこのタスクにおける定番の関数です。その使い方を見てみましょう。

NORM.DIST() 構文と引数

関数の構文は以下の通りです:

=NORM.DIST(x, mean, standard_dev, cumulative)

各引数を分解します:

• x: 分布を求めたい値。
• mean: 分布の平均。
• standard_dev: 分布の標準偏差。
• cumulative: 論理値—累積分布関数（CDF）の場合はTRUE、確率密度関数（PDF）の場合はFALSEを使用。

これを文脈に当てはめると、平均70、標準偏差10の正規分布において、値が80以下である確率を求めたいと想像してください。数式は以下のようになります:

=NORM.DIST(80, 70, 10, TRUE)

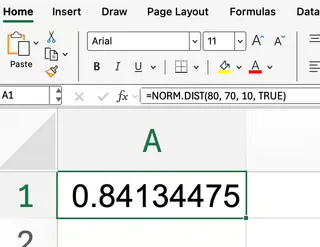
この設定は、80までの累積確率を返します。

累積確率 vs 確率密度

cumulative引数を理解することは、求めている結果を得るための鍵です。

• 累積 (TRUE): 最後の引数をTRUEに設定すると、NORM.DIST()は値がx以下である確率を返します。これは統計分析において最も一般的なオプションであり、「生徒の何パーセントが85点以下を取ったか？」のような質問に答えます。
• 確率密度 (FALSE): FALSEを選択すると、関数はxにおける正規曲線の高さを提供します。これは確率そのものではありませんが、統計モデリングや分布曲線のプロットに有用です。

方法 2: Excelmaticを使った現代的なAIアプローチ

構文をスキップして、必要なものをそのまま要求できたらどうでしょう？それがExcelmaticの出番です。Excel AIエージェントとして、平文のリクエストを即座な答え、チャート、洞察に変換します。

NORM.DIST関数とその4つの引数を覚える代わりに、単にあなたの要求を述べることができます。上記と同じシナリオ（平均=70、標準偏差=10、値=80）の場合、Excelmaticに次のように伝えます:

平均70、標準偏差10の正規分布において、値80の累積確率は何ですか？

Excelmaticはこのリクエストを処理し、数式を一度も入力することなく直接答えを提供します。このアプローチはより速いだけでなく、不正確な構文や引数の順序によって引き起こされるエラーも起こりにくくなります。

実践例: 並列比較

両方の方法が実際の問題を解決する様子を見てみましょう。

1. 累積確率を求める

テストスコアが平均75、標準偏差8の正規分布に従うと仮定して、テストスコアが85以下である確率を知りたいとします。

従来のNORM.DIST()法:

セルに次の数式を入力します:

=NORM.DIST(85, 75, 8, TRUE)

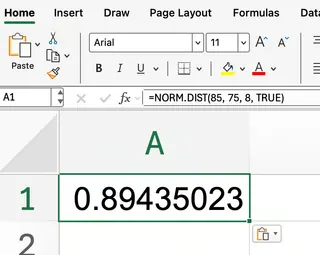
Excelは約0.894の値を返します。これは、約89.4%の生徒が85点以下を取ったことを意味します。

Excelmatic AI法:

単純に質問します:

スコアが平均75、標準偏差8の正規分布に従う場合、テストスコアが85以下である確率は何ですか？

Excelmaticは即座に同じ答え、0.894を提供し、数式を構築する時間と精神的努力を節約します。

2. 確率密度を取得する

では、累積確率ではなく、特定の値における曲線の高さに関心がある場合はどうでしょうか？

従来のNORM.DIST()法:

ここでは、cumulative引数をFALSEに設定します:

=NORM.DIST(85, 75, 8, FALSE)

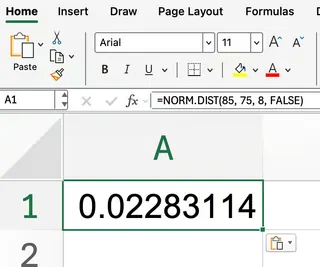
これは85における確率密度を与えます。これは確率ではなく、その点における正規曲線の値であることを忘れないでください。

Excelmatic AI法:

あなたの要求は同じくらい直接的です:

平均75、標準偏差8の正規分布において、値85における確率密度を計算してください。

再び、Excelmaticは背後で計算を処理し、正しい値を返します。以下の表は、両方のモードにおいて入力が出力にどのように影響するかをまとめています。

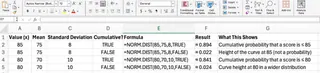
正規分布の可視化

ベルカーブを可視化することは、分布を理解するための素晴らしい方法です。ここでも、AIアプローチは大幅なショートカットを提供します。

従来法: 手動でのチャート作成

Excelでチャートを作成するには、まず手動でデータポイントを生成する必要があります:

1. x値の列を作成（例: 60から90まで1刻み）。
2. 数式を使用して累積値の2番目の列を作成: =NORM.DIST(x_cell, 75, 8, TRUE)。
3. 数式を使用して確率密度値の3番目の列を作成: =NORM.DIST(x_cell, 75, 8, FALSE)。
4. 3つの列すべてをハイライト。
5. 挿入 > グラフ > 折れ線グラフまたは平滑線散布図に移動してビジュアルを作成。

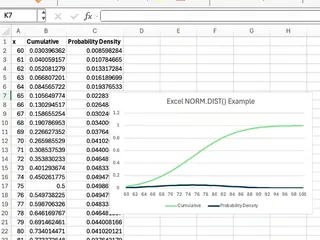
効果的ではありますが、このプロセスは複数ステップで時間がかかります。

Excelmatic法: 即時チャート生成

Excelmaticを使えば、手動でのデータ準備とチャート書式設定を回避できます。ただ質問してください:

平均75、標準偏差8の正規分布について、累積曲線と確率密度曲線を示す折れ線グラフを作成してください。x値は60から90を使用。

Excelmaticはデータとチャートを1ステップで生成し、同じプロフェッショナルな見た目のビジュアルをはるかに短時間で提供します。

NORM.DIST()関数に関する一般的な問題とヒント

従来の数式の道を選択する場合、いくつかの一般的な落とし穴に注意してください:

• 標準偏差は正でなければなりません。 ゼロまたは負の数を入力すると#NUM!エラーが発生します。
• 平均と標準偏差の柔軟性。 平均は任意の実数で構いませんが、標準偏差は常に正でなければなりません。
• 逆方向ですか？ 確率があり、対応する値を見つける必要がある場合は、代わりにNORM.INV()関数を使用してください。

Excelの関連関数

NORM.DIST()ファミリーには、統計分析に役立つ他のいくつかの関数が含まれます:

• NORM.INV(): NORM.DIST()の逆関数で、与えられた累積確率に対する値を返します。
• NORM.S.DIST(): 標準正規分布（平均=0、標準偏差=1）の確率を計算します。
• NORM.S.INV(): 標準正規分布における与えられた確率に対する値を返します。

それぞれの構文を学ぶこともできますが、ExcelmaticのようなAIツールも、単純な会話形式のリクエスト（例: 「標準正規分布を使用して、累積確率0.95に対応する値は何ですか？」）を通じてこれらのタスクを処理できることを忘れないでください。

結論

Excelで正規分布分析に取り組む2つの異なるが同等に強力な方法を見てきました。従来のNORM.DIST()関数は細かい制御を提供し、真剣なExcelユーザーにとって基本的なスキルです。同時に、ExcelmaticのようなAIエージェントは、複雑な統計タスクをより速く、より簡単に、誰にとってもよりアクセスしやすいものにすることで、データ分析に革命をもたらしています。

方法の選択はあなたのニーズによります。複雑で相互接続されたダッシュボードを構築している場合、数式が道筋となるかもしれません。しかし、迅速な分析、可視化、および構文で行き詰まることなく即座に答えを得るためには、AIアプローチが明らかな勝者です。

統計分析を簡素化する準備はできましたか？数式を暗記するのをやめて、質問を始めましょう。今すぐExcelmaticを試すと、必要な確率と洞察を即座に得られます。