Wichtigste Erkenntnisse:
- Die Berechnung der Standardabweichung ist entscheidend für die Bewertung der Volatilität von Geschäftskennzahlen wie Umsatz und Traffic. Traditionelle Excel-Methoden erfordern jedoch das Auswendiglernen komplexer Funktionen und statistischer Konzepte.
- Excelmatic ermöglicht komplexe Berechnungen wie die Standardabweichung durch einfache Sprachbefehle, eliminiert die Notwendigkeit, Formeln zu merken, und senkt die technische Hürde für die Datenanalyse.
- Im Vergleich zu manuellen Methoden identifiziert Excelmatic automatisch Datentypen und wendet die korrekte Formel an, während es gleichzeitig Visualisierungen generiert, was Effizienz und Genauigkeit erheblich steigert.
- Für Fachleute, die datengestützte Entscheidungen treffen müssen, verlagern Tools wie Excelmatic den Fokus von der technischen Umsetzung auf die Interpretation von Erkenntnissen und die Strategieentwicklung.
Die Standardabweichung zeigt uns, wie stark die Zahlen in einem bestimmten Datensatz streuen. Mehrere wichtige statistische Konzepte und Methoden, wie Varianz, Variationskoeffizient und Konfidenzintervalle, basieren auf der Standardabweichung als grundlegendes Maß für die Variabilität. Damit ist sie eines der wichtigsten Werkzeuge in der Statistik, das Datenprofis beherrschen müssen.
Dieser Artikel führt Sie in die Standardabweichung ein, zeigt Ihnen, wie Sie sie in Excel sowohl mit traditionellen Formeln als auch mit modernen KI-Tools berechnen, erklärt die Unterschiede zwischen den verfügbaren Methoden und demonstriert, wie Sie die Ergebnisse interpretieren, um fundierte Entscheidungen auf Grundlage Ihrer Analyse zu treffen.
Zwei Wege zur Berechnung der Standardabweichung in Excel
Wenn es um die Berechnung der Standardabweichung geht, haben Sie in Excel zwei Hauptwege: den modernen, konversationellen KI-Ansatz und die traditionelle, formelbasierte Methode.
Der KI-gestützte Weg: Verwendung von Excelmatic
Der schnellste und intuitivste Weg, die Aufgabe zu erledigen, ist mit einem KI-Agenten wie Excelmatic. Anstatt sich Funktionen und Syntax zu merken, fragen Sie einfach in einfacher Sprache nach dem, was Sie brauchen.
Mit Excelmatic ist der Prozess einfach:
- Laden Sie Ihre Excel-Datei mit dem Datensatz hoch.
- Stellen Sie eine direkte Frage, wie zum Beispiel:
- "Berechne die Standardabweichung für die täglichen Verkäufe in Spalte B."
- "Was ist die Stichproben-Standardabweichung meiner Verkaufsdaten?"
- "Zeig mir die Variabilität der täglichen Verkäufe."
Excelmatic erledigt alles andere. Es identifiziert automatisch die Daten, wendet die korrekte statistische Formel (Grundgesamtheit oder Stichprobe) an und liefert die Antwort sofort. Dieser Ansatz eliminiert die Notwendigkeit, sich den Unterschied zwischen STDEV.P und STDEV.S zu merken oder sich um Zellbereiche zu kümmern, spart Zeit und reduziert die Fehlerwahrscheinlichkeit.
Der traditionelle Formelweg: Verwendung von Excel-Funktionen
Um die Standardabweichung manuell in Excel zu berechnen, verwenden Sie die Funktion STDEV.P() für eine Grundgesamtheit oder die Funktion STDEV.S() für eine Stichprobe.

Wenn sich Ihre Daten beispielsweise in den Zellen B2 bis B31 befinden, würden Sie =STDEV.P(B2:B31) eingeben, um die Standardabweichung der Grundgesamtheit zu berechnen, oder =STDEV.S(B2:B31) für die Standardabweichung der Stichprobe. Excel berechnet und zeigt dann das Ergebnis an. Diese Methode ist zwar effektiv, erfordert aber, dass Sie wissen, welche Funktion für Ihre Daten geeignet ist.
Was ist die Standardabweichung?
Die Standardabweichung ist ein statistisches Maß, das die Menge der Variation oder Streuung in einer Menge numerischer Werte quantifiziert. Sie gibt an, wie stark die Werte in einem Datensatz vom Mittelwert (Durchschnitt) des Datensatzes abweichen.
Sie hilft, das Ausmaß der Variabilität innerhalb von Daten zu verstehen – eine niedrige Standardabweichung zeigt an, dass die Werte nahe am Mittelwert liegen, was auf Konsistenz hindeutet, während eine hohe Standardabweichung auf eine größere Variabilität hindeutet, was stärker gestreute Daten bedeutet.
Formeln für die Standardabweichung
Die Formel für die Standardabweichung hängt davon ab, ob wir es mit einer Grundgesamtheit oder einer Stichprobe zu tun haben. Die Formel für die Standardabweichung der Grundgesamtheit (σ) lautet wie folgt:
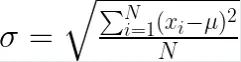
Dabei gilt:
Nist die Gesamtzahl der Datenpunkte in der Grundgesamtheit.x_i repräsentiert jeden einzelnen Datenpunkt.μist der Mittelwert (Durchschnitt) der Grundgesamtheit.
Diese Formel berechnet den Durchschnitt der quadrierten Abweichungen vom Mittelwert und zieht dann die Quadratwurzel aus diesem Durchschnitt.
Die Formel für die Standardabweichung der Stichprobe (s) lautet wie folgt. Beachten Sie, dass wir für die Stichproben-Standardabweichung der Konvention folgend ein kleines n verwenden.
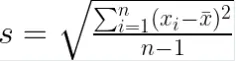
Dabei gilt:
nist die Gesamtzahl der Datenpunkte in der Stichprobe.x_i repräsentiert jeden einzelnen Datenpunkt.xˉist der Mittelwert (Durchschnitt) der Stichprobe.
Die Formel ähnelt der für die Standardabweichung der Grundgesamtheit. Sie verwendet jedoch n - 1 (Besselsche Korrektur) im Nenner, um der Tatsache Rechnung zu tragen, dass eine Stichprobe zur Schätzung des Populationsparameters verwendet wird. Diese Korrektur macht die Stichproben-Standardabweichung zu einem erwartungstreuen Schätzer für die Standardabweichung der Grundgesamtheit.
Praktische Anwendungen der Standardabweichung
Die Standardabweichung ist eine häufig verwendete Technik in verschiedenen Bereichen. Sie liefert wertvolle Einblicke in die Datenvariabilität und -konsistenz und kann in verschiedenen Domänen angewendet werden, darunter:
- Risikobewertung: Die Standardabweichung kann die Volatilität von Vermögensrenditen messen. Eine höhere Standardabweichung deutet auf ein größeres Risiko und eine größere potenzielle Variabilität der Rendite hin.
- Qualitätskontrolle: Die Fertigungsindustrie verwendet die Standardabweichung, um die Produktqualität zu überwachen und zu steuern und so Konsistenz und Einhaltung von Standards sicherzustellen.
- Gesundheitswesen und Medizin: Die Standardabweichung wird verwendet, um die Streuung von Daten wie dem Blutdruck oder Cholesterinspiegel von Patienten zu verstehen, was hilft, Ausreißer und Normalbereiche zu identifizieren.
- Bildung & Forschung: Die Standardabweichung hilft, die Verteilung von Testergebnissen zu bestimmen und die Wirksamkeit pädagogischer Interventionen zu bewerten.
- Wetter- und Klimastudien: Meteorologen verwenden die Standardabweichung, um Wetterdaten wie Temperatur und Niederschlag zu analysieren, um die Klimavariabilität zu verstehen.
Arten von Standardabweichungsfunktionen in Excel
Microsoft Excel verfügt über zwei verschiedene Funktionen zur Berechnung der Standardabweichung, je nachdem, ob Sie mit einer gesamten Grundgesamtheit oder einer Stichprobe arbeiten.
STDEV.P() für die Standardabweichung der Grundgesamtheit
Die Funktion STDEV.P() in Excel berechnet die Standardabweichung für eine gesamte Grundgesamtheit. Diese Funktion geht davon aus, dass die bereitgestellten Argumente die gesamte Grundgesamtheit enthalten. Die Syntax für die Funktion STDEV.P() lautet wie folgt:
STDEV.P(number1, [number2], ...)
Die Parameter sind:
number1: Das erste Zahlenargument, das einer Grundgesamtheit entspricht.[number2], ...: Optionale zusätzliche Zahlen oder Bezüge, die einer Grundgesamtheit entsprechen, bis zu 254 Argumente.
Sie sollten STDEV.P() verwenden, wenn Ihre Daten die gesamte interessierende Grundgesamtheit darstellen, zum Beispiel die Testergebnisse aller Schüler einer bestimmten Schule.
STDEV.S() für die Standardabweichung der Stichprobe
Die Funktion STDEV.S() in Excel berechnet die Standardabweichung für eine Stichprobe aus der Grundgesamtheit. Diese Funktion geht davon aus, dass die bereitgestellten Argumente eine Stichprobe der Grundgesamtheit und nicht die gesamte Grundgesamtheit sind. Die Syntax für die Funktion STDEV.S() lautet wie folgt:
STDEV.S(number1, [number2], ...)
Die Parameter sind:
number1: Das erste Zahlenargument, das einer Stichprobe der Grundgesamtheit entspricht.[number2], ...: Optionale zusätzliche Zahlen oder Bezüge, die einer Stichprobe entsprechen, bis zu 254 Argumente.
In der Praxis verwenden wir STDEV.S(), um die Standardabweichung der gesamten Grundgesamtheit zu schätzen, wenn wir eine Stichprobe von Daten haben. Wenn Sie beispielsweise die Testergebnisse einer zufällig ausgewählten Teilmenge von Schülern einer Schule analysieren, ist STDEV.S() die richtige Wahl.
Berechnung der Standardabweichung: Ein praktisches Beispiel
Stellen Sie sich vor, Sie sind ein Datenanalyst, der mit der Analyse der Verkaufsleistung eines kleinen Einzelhandelsgeschäfts beauftragt ist. Der Eigentümer möchte die Variabilität der täglichen Verkäufe im vergangenen Monat verstehen, um Lagerbestand und Personal besser zu managen.
Sie haben die täglichen Verkaufsdaten für 30 Tage gesammelt. Lassen Sie uns diese Aufzeichnungen in eine Spalte, sagen wir B2 bis B31, in einer Excel-Tabelle eintragen.
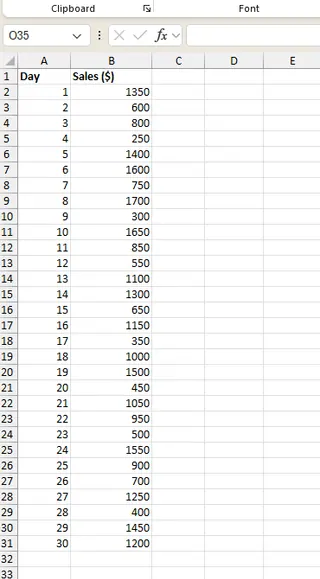
Vergleichen wir die beiden Methoden, um die Standardabweichung zu finden.
Methode 1: Der traditionelle Formelansatz
Da unsere Analyse die gesamten monatlichen Verkaufsdaten abdeckt (unsere vollständige interessierende Grundgesamtheit), verwenden wir die Funktion STDEV.P(). Geben Sie in Zelle E6 die folgende Formel ein:
=STDEV.P(B2:B31)
Excel berechnet die Standardabweichung der Grundgesamtheit.
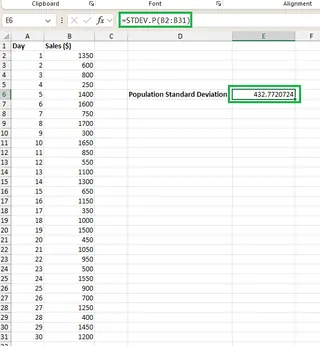
Nehmen wir nun an, wir würden diese 30-Tage-Daten als Stichprobe verwenden, um die Leistung für das gesamte Jahr zu schätzen. Wir würden stattdessen die Funktion STDEV.S() verwenden:
=STDEV.S(B2:B31)
Dies würde uns die Standardabweichung der Stichprobe liefern.
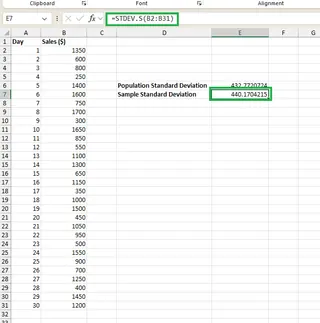
Methode 2: Der Excelmatic-KI-Ansatz
Mit Excelmatic würden Sie einfach die Tabelle hochladen und fragen:
Berechne die Standardabweichung der Grundgesamtheit für die Daten in B2:B31.
Oder, wenn Sie sie als Stichprobe behandeln:
Was ist die Standardabweichung der Stichprobe für die täglichen Verkäufe?
Excelmatic liefert die Antwort sofort, ohne dass Sie eine Funktion auswählen oder eine Formel eingeben müssen. Dies ist besonders nützlich, wenn Sie unsicher sind, welche Formel Sie verwenden sollen, da Sie Ihr Ziel beschreiben können und die KI die statistischen Details übernimmt.
Interpretation von Standardabweichungswerten
Nach der Berechnung der Standardabweichung ist der nächste Schritt die Interpretation des Ergebnisses. Um dies effektiv zu tun, ist es hilfreich, auch den Mittelwert (Durchschnitt) der Daten zu kennen.
Sie können dies in Excel mit =AVERAGE(B2:B31) berechnen oder indem Sie Excelmatic fragen: "Was ist der Durchschnitt der täglichen Verkäufe?".
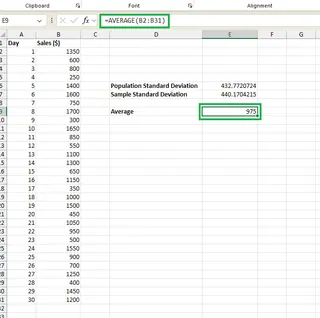
Mit einem Mittelwert von 975 $ können wir die Standardabweichungswerte interpretieren:
- Standardabweichung der Grundgesamtheit (~432,77 $): Dies zeigt an, dass die täglichen Verkäufe im Durchschnitt um etwa 432,77 $ vom Mittelwert von 975 $ abweichen. Diese Zahl repräsentiert die Streuung der Verkaufsdaten für diesen spezifischen Monat.
- Standardabweichung der Stichprobe (~440,17 $): Dieser Wert ist etwas höher. Er ist die relevante Zahl, wenn wir diese 30 Tage als Stichprobe behandeln, um die Variabilität für einen größeren Zeitraum (z.B. das gesamte Jahr) zu schätzen. Der höhere Wert berücksichtigt die Unsicherheit der Verwendung einer Stichprobe.
- Hohe Variabilität der Verkäufe: Beide Werte deuten auf eine hohe Variabilität hin. Die Verkäufe schwanken erheblich vom Durchschnitt, was sich auf Lagerbestand und Personal auswirken könnte. Diese Inkonsistenz legt nahe, dass weitere Analysen erforderlich sein könnten, um die täglichen Verkäufe genauer vorherzusagen.
Der Geschäftsinhaber sollte diese Variabilität bei der Planung berücksichtigen, um Überbestände an langsamen Tagen oder Unterbesetzung an geschäftigen Tagen zu vermeiden.
So fügen Sie Standardabweichungsbalken in Excel hinzu
Die Visualisierung von Variabilität ist wirkungsvoll. Das Hinzufügen von Standardabweichungsbalken zu einem Diagramm in Excel ist eine großartige Möglichkeit, dies zu tun.
Der KI-Weg: Excelmatic
Dies ist ein weiterer Bereich, in dem ein KI-Agent glänzt. Fragen Sie einfach:
Erstelle ein Liniendiagramm der täglichen Verkäufe mit Standardabweichungs-Fehlerbalken.
Excelmatic generiert das vollständige Diagramm für Sie in einem einzigen Schritt.
Der traditionelle Weg: Manuelles Erstellen von Diagrammen in Excel
- Wählen Sie Ihren Datenbereich aus (B2 bis B31).
- Gehen Sie zur Registerkarte Einfügen und wählen Sie einen Diagrammtyp (z.B. ein Liniendiagramm).
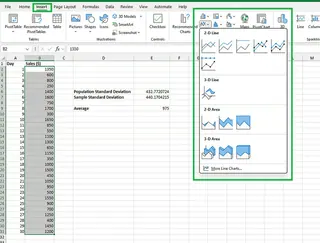
Sie erhalten ein einfaches Liniendiagramm.
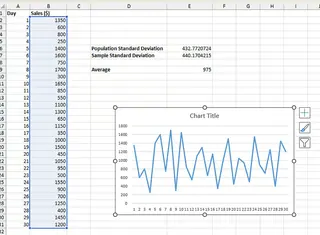
- Klicken Sie auf das Diagramm, um die Registerkarte Diagrammentwurf aufzurufen.
- Klicken Sie auf Diagrammelement hinzufügen > Fehlerbalken > Standardabweichung.
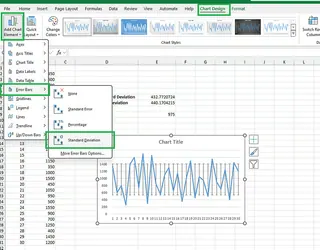
- Zur Anpassung können Sie Weitere Fehlerbalkenoptionen... auswählen, um das Erscheinungsbild zu ändern.
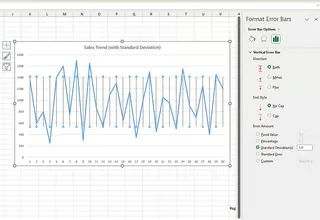
Beim Vergleich der beiden Methoden ist der KI-Ansatz eindeutig schneller und erfordert keine Navigation durch Menüs.
Fazit
Die Beherrschung der Standardabweichung ist grundlegend für eine robuste Datenanalyse und liefert kritische Einblicke in die Variabilität. Dieser Leitfaden hat zwei unterschiedliche Ansätze innerhalb von Excel demonstriert: die grundlegende Präzision der integrierten Funktionen (STDEV.P, STDEV.S) und die moderne Effizienz KI-gestützter Tools.
Die Entwicklung von der manuellen Formeleingabe zur konversationellen KI, wie sie von Excelmatic verkörpert