Wichtigste Erkenntnisse:
- Die Berechnung von Quadratwurzeln in Excel ist für Geometrie, Statistik und Finanzen unerlässlich, aber traditionelle Methoden erfordern technisches Wissen über Formeln wie
SQRT()undPOWER(). - Excelmatic bietet eine einfachere Lösung, indem es Quadratwurzelberechnungen sofort mit einfachen Sprachbefehlen durchführt – ohne Formelsyntax.
- Im Vergleich zu formelbasierten Ansätzen bewältigt Excelmatic große Datensätze und komplexe mehrstufige Anfragen mühelos und eliminiert manuelle Einrichtung und Fehlerbehebung.
- Für Geschäftsanwender, die schnelle Berechnungen benötigen, bedeuten KI-Tools wie Excelmatic schnellere Ergebnisse und mehr Zeit für die Analyse statt für die technische Umsetzung.
Die Berechnung einer Quadratwurzel ist eine grundlegende Aufgabe in der Datenanalyse, sei es für geometrische Probleme, statistische Berechnungen oder Finanzmodellierung. Excel bietet leistungsstarke Werkzeuge dafür, aber die beste Methode hängt von Ihrem Arbeitsablauf ab.
Traditionell bedeutete dies die Verwendung eingebauter Funktionen wie SQRT(). Sie ist schnell, zuverlässig und lässt sich leicht in andere Formeln integrieren. Moderne KI-Tools bieten jedoch heute einen völlig anderen Ansatz – einen, der einfache Sprache anstelle von Syntax verwendet.
In diesem Leitfaden vergleichen wir zwei leistungsstarke Methoden zum Finden einer Quadratwurzel in Excel: den klassischen formelbasierten Ansatz und die moderne, konversationelle KI-Methode mit Excelmatic.
Methode 1: Der traditionelle Formelansatz mit SQRT()
Der direkteste Weg, eine Quadratwurzel in Excel zu berechnen, ist mit der Funktion SQRT(). Sie ist für einen Zweck konzipiert: die positive Quadratwurzel einer positiven Zahl zurückzugeben.
Wie funktioniert SQRT()?
Die Syntax ist einfach und unkompliziert:
=SQRT(Zahl)
Hierbei kann Zahl ein direkter Wert, ein Zellbezug oder sogar das Ergebnis einer anderen Formel sein.
Wann sollten Sie SQRT() verwenden?
Immer wenn Sie die positive Quadratwurzel einer positiven Zahl benötigen, ist diese Funktion eine gute Wahl. Sie ist üblich in der Geometrie (z.B. um die Seitenlänge eines Quadrats aus seiner Fläche zu ermitteln), Statistik und Finanzen.
Einfache SQRT()-Beispiele
Sehen wir uns an, wie sie in der Praxis funktioniert.
Die Quadratwurzel einer Zahl finden
Um die Quadratwurzel von 25 zu berechnen, würden Sie dies in eine beliebige Zelle eingeben:
=SQRT(25)
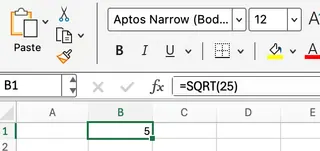
Excel gibt korrekt 5 zurück. Dies ist die Grundlage für dynamischere Berechnungen.
Einen Zellbezug verwenden
In den meisten Tabellen sind Ihre Daten nicht fest codiert. Wenn Zelle A1 die Zahl 81 enthält, können Sie einen Zellbezug verwenden:
=SQRT(A1)
Diese Formel gibt 9 zurück. Die Verwendung von Zellbezügen macht Ihr Arbeitsblatt dynamisch – wenn sich der Wert in A1 ändert, aktualisiert sich das Ergebnis automatisch.
SQRT() mit anderen Formeln kombinieren
Sie können Berechnungen auch direkt in die SQRT()-Funktion einbetten. Um beispielsweise die Quadratwurzel der Summe von A1 und B1 zu finden:
=SQRT(A1 + B1)
Dies ist nützlich, wenn Ihr Eingabewert von anderen Datenpunkten abgeleitet wird.
Eine alternative Formel: POWER()
Eine andere Möglichkeit, eine Quadratwurzel zu berechnen, ist die Funktion POWER(), die eine Zahl mit einem gegebenen Exponenten potenziert. Da eine Quadratwurzel dasselbe ist wie das Potenzieren einer Zahl mit 0,5, können Sie verwenden:
=POWER(A1, 0.5)

Während dies perfekt funktioniert, ist SQRT(A1) lesbarer und direkter, wenn Sie nur eine Quadratwurzel benötigen. POWER() wird nützlicher, wenn es um Kubikwurzeln oder andere gebrochene Exponenten geht.
Fehlerbehandlung und Einschränkungen bei Formeln
Die größte Einschränkung von SQRT() ist, dass sie keine negativen Zahlen verarbeiten kann, da deren Quadratwurzeln keine reellen Zahlen sind. Der Versuch, =SQRT(-9) zu berechnen, führt zu einem #NUM!-Fehler.
Um dies zu vermeiden, können Sie eine Sicherung mit der IF()-Funktion einbauen:
=IF(A1 < 0, "Ungültige Zahl", SQRT(A1))
Diese Formel prüft zuerst, ob die Zahl in A1 negativ ist. Wenn ja, gibt sie "Ungültige Zahl" zurück; andernfalls fährt sie mit der Berechnung fort. Dies ist effektiv, erhöht aber die Komplexität Ihrer Formeln.
Methode 2: Der KI-gestützte Ansatz mit Excelmatic
Was wäre, wenn Sie die Formeln ganz überspringen könnten? Excelmatic ist ein Excel-KI-Agent, mit dem Sie Berechnungen durchführen, Daten analysieren und Diagramme erstellen können, indem Sie einfach in einfacher Sprache fragen.
Anstatt sich Funktionen und Syntax zu merken, geben Sie einfach Ihre Anfrage ein.
Wie funktioniert Excelmatic?
Der Prozess ist erfrischend einfach:
- Laden Sie Ihre Excel-Datei(en) in Excelmatic hoch.
- Geben Sie Ihre Anfrage in das Chat-Feld ein, genau wie bei der Kommunikation mit einem menschlichen Analysten.
- Excelmatic verarbeitet die Anfrage und liefert sofort die Antwort, die aktualisierte Tabelle oder das Diagramm.
Um eine Quadratwurzel zu berechnen, könnten Sie ein Blatt mit einer Liste von Zahlen in Spalte A hochladen und einfach fragen:
Berechne die Quadratwurzel für alle Werte in Spalte A und schreibe die Ergebnisse in eine neue Spalte namens 'Quadratwurzel'.
Excelmatic erledigt den Rest. Es gibt keine Formel einzutippen, keine Syntax zu merken und keine Notwendigkeit, Zellen durch Ziehen zu füllen.
Wann sollten Sie Excelmatic verwenden?
Excelmatic glänzt dort, wo Formeln umständlich werden.
- Für Anfänger: Es beseitigt die Hürde, die Excel-Funktionsbibliothek zu erlernen.
- Für große Datensätze: Ein einzelner Befehl kann Tausende von Zeilen verarbeiten und erspart Ihnen die manuelle Formeleingabe und das Ziehen.
- Für komplexe Anfragen: Sie können Befehle verketten. Zum Beispiel: "Berechne die Quadratwurzel für Spalte A, dann finde den Durchschnitt der Ergebnisse."
- Für die Fehlerbehandlung: Excelmatic kann Kontext interpretieren. Wenn Sie negative Zahlen haben, kann es zur Klärung auffordern oder sie automatisch kennzeichnen und so die abrupten
#NUM!-Fehler vermeiden, die Sie mitSQRT()erhalten.
Vergleich der Methoden: Formeln vs. KI
| Merkmal | Traditionelle Formeln (SQRT()) |
KI-Agent (Excelmatic) |
|---|---|---|
| Benutzerfreundlichkeit | Erfordert Kenntnis der Funktionssyntax (=SQRT(A1)). |
Verwendet einfache Sprache. Keine Syntax erforderlich. |
| Geschwindigkeit | Schnell für Einzelberechnungen. Kann für große Datensätze langsam sein (Ziehen zum Ausfüllen). | Sofortig für Einzelberechnungen und große Datensätze. |
| Fehlerbehandlung | Gibt Fehler wie #NUM! zurück. Erfordert manuelle Workarounds (z.B. IF-Anweisungen). |
Intuitiver. Kann Probleme kennzeichnen oder zur Klärung auffordern. |
| Flexibilität | Hervorragend für die Integration in komplexe, verschachtelte Formeln. | Hervorragend für mehrstufige Datenaufgaben und schnelle Analysen ohne Einrichtung. |
| Lernkurve | Mittel. Sie müssen spezifische Funktionen und ihre Grenzen lernen. | Minimal. Wenn Sie eine Frage stellen können, können Sie es verwenden. |
Praxisbeispiele: Ein direkter Vergleich
Kehren wir zu unseren Praxisbeispielen zurück, um zu sehen, wie die beiden Methoden abschneiden.
Geometrie: Berechnung der Diagonale eines Quadrats
Sie haben eine Liste von Seitenlängen in Spalte A und müssen die Diagonale finden. Die mathematische Formel ist d = Seite × √2.
SQRT()-Methode: In Zelle B1 würden Sie=A1 * SQRT(2)eingeben und die Formel die Spalte hinunterziehen.- Excelmatic-Methode: Sie würden einfach fragen: "Multipliziere für die Seitenlängen in Spalte A jede mit der Quadratwurzel von 2 und zeige das Ergebnis in einer neuen Spalte 'Diagonale'."
Statistik: Berechnung der Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz. Wenn Sie die Varianz in Zelle B1 haben:
SQRT()-Methode: Sie würden=SQRT(B1)eingeben. Natürlich könnten Sie auch die speziellen FunktionenSTDEV.P()oderSTDEV.S()verwenden, wenn Sie sie kennen.- Excelmatic-Methode: Sie können die Zwischenschritte überspringen und direkt fragen: "Berechne die Standardabweichung für die Daten in Spalte B." Excelmatic versteht das statistische Konzept und führt die korrekte Berechnung durch, ohne dass Sie die zugrundeliegende Formel kennen müssen.
Fazit: Welche Methode ist die richtige für Sie?
Zu wissen, wie man Funktionen wie SQRT() und POWER() verwendet, ist eine Kernkompetenz in Excel. Sie geben Ihnen detaillierte Kontrolle über Ihre Berechnungen und sind unerlässlich für den Aufbau komplexer, vernetzter Tabellen. Für schnelle Einzelberechnungen oder beim Erstellen eines dynamischen Finanzmodells sind Formeln nach wie vor unschlagbar.
Die Landschaft der Datenanalyse verändert sich jedoch. KI-Agenten wie Excelmatic führen ein neues Niveau an Geschwindigkeit und Zugänglichkeit ein. Indem sie die Verwendung natürlicher Sprache ermöglichen, beseitigen sie die Notwendigkeit, sich Syntax zu merken und komplexe Fehlerbehandlungsformeln zu erstellen. Für das Bereinigen von Daten, die Durchführung mehrstufiger Analysen oder einfach das schnelle Erhalten von Antworten aus Ihrer Tabelle ist der KI-Ansatz oft schneller und intuitiver.
Der beste Ansatz ist, beides in Ihrem Werkzeugkasten zu haben. Beherrschen Sie die Formeln für die Kontrolle und nutzen Sie KI, um Ihren Arbeitsablauf schneller und intelligenter zu gestalten.
Bereit, schneller und intelligenter zu berechnen? Testen Sie Excelmatic noch heute und führen Sie komplexe Berechnungen wie Quadratwurzeln mit einer einfachen Anfrage durch.






