Wichtige Erkenntnisse:
- Die manuelle Berechnung von Kreditraten in Excel mit der
PMT()-Funktion ist aufgrund komplexer Syntax, obligatorischer Zinssatz-/Laufzeitanpassungen und verwirrender Vorzeichenkonventionen fehleranfällig. - Excelmatic vereinfacht diesen Prozess vollständig, indem Sie Finanzfragen in natürlicher Sprache stellen können (z.B. "Wie hoch ist meine monatliche Hypothekenzahlung?"), und sofortige, genaue Antworten ohne Formeln liefert.
- Das KI-gestützte Tool glänzt bei komplexen Aufgaben wie der Erstellung vollständiger Tilgungspläne und der Durchführung von "Was-wäre-wenn"-Analysen mit einer einzigen Eingabe und übersetzt so komplexe manuelle Arbeit in einfache Gespräche.
- Für Fachleute, die zuverlässige Finanzberechnungen ohne technischen Aufwand benötigen, ist die Nutzung von Excelmatic der schnellste Weg von Finanzfragen zu umsetzbaren Erkenntnissen.
Excel ist ein Kraftpaket für Finanzberechnungen, von einfachem Budgeting bis hin zu komplexen Unternehmensfinanzmodellen. Eine der grundlegendsten Aufgaben ist die Berechnung periodischer Zahlungen für einen Kredit oder eine Investition. Traditionell erforderte dies die Beherrschung von Excels PMT()-Funktion, einem vielseitigen Werkzeug für jeden, der sich mit Hypotheken, Krediten oder Sparplänen befasst.
Allerdings verändert sich die Landschaft der Datenanalyse. Während das Verständnis der Mechanik von Finanzfunktionen wertvoll ist, bieten moderne KI-Tools einen schnelleren, intuitiveren Weg zu denselben Antworten.
Diese Anleitung untersucht beide Methoden. Wir gehen durch die traditionelle Art der Verwendung der PMT()-Funktion und ihrer verwandten Formeln. Dann stellen wir eine intelligentere Alternative vor – die Verwendung eines KI-Agenten wie Excelmatic – um Ihnen zu zeigen, wie Sie sofortige Finanzeinblicke erhalten können, indem Sie einfach Fragen in einfacher Sprache stellen.
Zwei Wege zu Ihrer Antwort
Nehmen wir an, Sie möchten die monatliche Rate für eine typische 30-jährige Hypothek von 300.000 $ mit einem jährlichen Zinssatz von 4,5 % berechnen.
Die traditionelle Formelmethode
In einem standardmäßigen Excel-Blatt würden Sie die PMT()-Funktion verwenden und dabei sorgfältig Zinssatz und Laufzeit für monatliche Zahlungen anpassen. Die Formel wäre:
=PMT(4.5%/12, 30*12, 300000)
Dies ergibt eine monatliche Rate von ungefähr 1.520,06 $.
Die KI-Agenten-Methode (mit Excelmatic)
Mit einem KI-Agenten wie Excelmatic laden Sie einfach Ihre Tabelle hoch (oder haben die Daten griffbereit) und stellen eine direkte Frage:
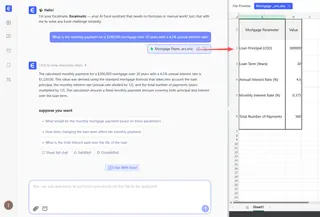
Wie hoch ist die monatliche Rate für eine Hypothek von 300.000 $ über 30 Jahre mit einem jährlichen Zinssatz von 4,5 %?
Excelmatic verarbeitet Ihre Anfrage sofort, führt die Berechnung durch und gibt Ihnen die Antwort, ohne dass Sie jemals eine Formel anfassen müssen.
Lassen Sie uns nun tiefer in die Details der traditionellen Methode eintauchen, bevor wir weitere KI-gestützte Abkürzungen erkunden.
Die traditionelle Methode: Die PMT()-Funktion verstehen
Die PMT()-Funktion in Excel berechnet die periodische Zahlung, die erforderlich ist, um einen Kredit oder eine Investition mit konstanten Zahlungen und einem festen Zinssatz zu begleichen.
PMT()-Funktionssyntax und Parameter
Die Syntax der PMT()-Funktion lautet:
=PMT(rate, nper, pv, [fv], [type])
Lassen Sie uns jeden Parameter aufschlüsseln:
rate: Der Zinssatz für jede Periode. Wenn Ihr Kredit einen jährlichen Zinssatz von 4,5 % hat, die Zahlungen jedoch monatlich erfolgen, müssen Sie4.5%/12verwenden.nper: Die Gesamtzahl der Zahlungsperioden. Für einen 30-jährigen Kredit mit monatlichen Zahlungen würden Sie30*12oder 360 Perioden verwenden.pv: Der Barwert oder der Gesamtbetrag, den eine Reihe zukünftiger Zahlungen jetzt wert ist. Für einen Kredit ist dies der aufgenommene Kapitalbetrag.fv(optional): Der zukünftige Wert oder ein Geldbetrag, den Sie nach der letzten Zahlung erreichen möchten. Wenn er weggelassen wird, standardmäßig0(was bedeutet, dass der Kredit vollständig zurückgezahlt ist).type(optional): Eine Zahl, die angibt, wann Zahlungen fällig sind. Verwenden Sie0für Zahlungen am Ende der Periode (Standard) oder1für Zahlungen am Anfang.
Es ist wichtig, die Cashflow-Konvention in Excel zu verstehen: Geld, das Sie ausgeben (wie eine Kreditzahlung), wird durch eine negative Zahl dargestellt, während Geld, das Sie erhalten (wie der anfängliche Kreditbetrag), positiv ist. Deshalb sind PMT()-Ergebnisse typischerweise negativ.
Zahlungshäufigkeitsanpassungen verstehen
Eine häufige Fehlerquelle ist das Versäumnis, die Argumente rate und nper an die Zahlungshäufigkeit anzupassen. Die meisten Kredite haben einen jährlichen Zinssatz, aber die Zahlungen erfolgen monatlich. Sie müssen sich entsprechend anpassen.
- Monatlich:
Jährlicher Zinssatz / 12,Anzahl der Jahre * 12 - Vierteljährlich:
Jährlicher Zinssatz / 4,Anzahl der Jahre * 4 - Halbjährlich:
Jährlicher Zinssatz / 2,Anzahl der Jahre * 2
Diese Tabelle fasst die Anpassungen für einen 5-jährigen Kredit mit einem jährlichen Zinssatz von 6 % zusammen:
| Zahlungshäufigkeit | Zinssatzanpassung | Laufzeitanpassung | Angepasster Zinssatz | Angepasste Perioden |
|---|---|---|---|---|
| Monatlich | Jährlich ÷ 12 | Jahre × 12 | 0,5% | 60 |
| Vierteljährlich | Jährlich ÷ 4 | Jahre × 4 | 1,5% | 20 |
| Halbjährlich | Jährlich ÷ 2 | Jahre × 2 | 3% | 10 |
| Jährlich | Keine Änderung | Keine Änderung | 6% | 5 |
Diese Anpassungen korrekt vorzunehmen, ist entscheidend für eine genaue Berechnung.
Häufige Anwendungen: Der alte Weg vs. der neue Weg
Lassen Sie uns sehen, wie beide Methoden die beiden häufigsten Finanzberechnungen handhaben.
Hypothekenraten berechnen
Gehen wir ein Beispiel aus dem echten Leben durch:
- Kreditbetrag: 400.000 $
- Zinssatz: 6 % jährlich
- Kreditlaufzeit: 20 Jahre
- Zahlungshäufigkeit: Monatlich
Die traditionelle Methode: Verwendung der PMT()-Funktion
Zuerst müssen wir Zinssatz und Perioden anpassen:
- Angepasster Zinssatz:
6%/12(0,5 % pro Monat) - Angepasste Perioden:
20*12(240 Monate)
Die Formel wäre:
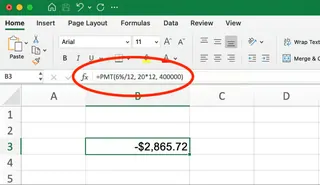
=PMT(6%/12, 20*12, 400000)
Dies ergibt ein Ergebnis von -2.865,72 $. Dies ist Ihre monatliche Hypothekenzahlung.
Die KI-Abkürzung: Verwendung von Excelmatic
Mit Excelmatic überspringen Sie die manuellen Anpassungen. Sie fragen einfach:
Berechnen Sie die monatliche Rate für einen Kredit von 400.000 $ über 20 Jahre mit einem jährlichen Zinssatz von 6 %.
Excelmatic interpretiert Ihre Anfrage, versteht, dass "jährlicher Zinssatz" und "monatliche Zahlung" eine Anpassung erfordern, und liefert sofort die korrekte Antwort von 2.865,72 $.
Spar- und Investitionsbeiträge berechnen
Die PMT()-Funktion kann auch berechnen, wie viel Sie regelmäßig sparen müssen, um ein zukünftiges finanzielles Ziel zu erreichen.
Angenommen, Sie möchten in 18 Jahren 50.000 $ sparen, mit einer geschätzten jährlichen Rendite von 6 %, und Sie zahlen monatlich ein.
Die traditionelle Methode: Verwendung der PMT()-Funktion
In diesem Fall ändern sich die Parameter:
- Zukünftiger Wert (fv):
50000(Ihr Ziel) - Barwert (pv):
0(Sie fangen bei Null an) - Zinssatz:
6%/12(0,5 % monatlich) - Perioden:
18*12(216 Monate)
Die Formel wäre:
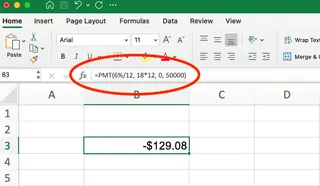
=PMT(6%/12, 18*12, 0, 50000)
Dies gibt -129,08 $ zurück, was bedeutet, dass Sie monatlich etwa 130 $ einzahlen müssen, um Ihr Ziel zu erreichen.
Die KI-Abkürzung: Verwendung von Excelmatic
Wieder können Sie eine einfache, konversationsähnliche Eingabe verwenden:
Wie viel muss ich monatlich sparen, um in 18 Jahren 50.000 $ zu haben, bei einer angenommenen jährlichen Rendite von 6 %?
Excelmatic versteht das Ziel und liefert den erforderlichen monatlichen Beitrag, ohne dass Sie sich merken müssen, welcher Parameter pv und welcher fv ist.
Häufige Fehler und wie man sie vermeidet
Die Arbeit mit der PMT()-Funktion kann knifflig sein. Hier sind häufige Fallstricke:
#NUM!- oder#WERT!-Fehler: Diese treten oft aufgrund ungültiger Eingaben auf, wie Text in einem Zahlenfeld oder ein so niedriger Zinssatz, dass der Kredit nie zurückgezahlt werden kann.- Vergessen von Häufigkeitsanpassungen: Der häufigste Fehler ist die Verwendung eines jährlichen Zinssatzes (z.B.
6%) für monatliche Zahlungen anstelle des monatlichen Zinssatzes (6%/12). - Falsche Vorzeichen: Das Vergessen, dass ausgehende Zahlungen negativ sind, kann zu verwirrenden Ergebnissen führen.
- Vermischung von Perioden: Sicherzustellen, dass
npermit derrate-Periode übereinstimmt (z.B. beide monatlich), ist entscheidend.
Hier bietet ein KI-Agent einen erheblichen Vorteil. Durch die Interpretation natürlicher Sprache eliminiert Excelmatic Syntaxfehler, Parameterverwechslungen und Häufigkeitsanpassungsfehler, da es die technische Übersetzung im Hintergrund handhabt.
Erweiterte Analyse: Eine Funktionsfamilie vs. eine einzige KI
Die PMT()-Funktion ist nur ein Mitglied von Excels Finanzfunktionsfamilie. Um ein vollständiges Bild eines Kredits zu erhalten, müssen Sie oft mehrere andere verwenden.
| Funktion | Was sie tut | Traditionelle Excel-Formel | Excelmatic-Eingabe |
|---|---|---|---|
| IPMT() | Berechnet den Zinsanteil einer bestimmten Zahlung. | =IPMT(rate, per, nper, pv) |
"Wie viel meiner 12. Zahlung ist Zins?" |
| PPMT() | Berechnet den Tilgungsanteil einer bestimmten Zahlung. | =PPMT(rate, per, nper, pv) |
"Wie viel meiner 12. Zahlung geht in die Tilgung?" |
| NPER() | Berechnet die Anzahl der Perioden, um einen Kredit abzuzahlen. | =NPER(rate, pmt, pv) |
"Wie lange dauert es, meinen Kredit abzuzahlen, wenn ich 2000 $/Monat zahle?" |
| RATE() | Berechnet den Zinssatz eines Kredits. | =RATE(nper, pmt, pv)*12 |
"Wie hoch ist der Zinssatz für einen 30-jährigen, 300.000 $-Kredit mit 1520 $-Zahlungen?" |
Der KI-Vorteil: Von einzelnen Antworten zu vollständigen Berichten
Während Sie eine Analyse mit diesen einzelnen Funktionen zusammensetzen können, ist es zeitaufwändig. Ein KI-Agent kann viel weiter und viel schneller gehen. Zum Beispiel könnten Sie anstatt IPMT und PPMT für jede Periode zu berechnen, einfach Excelmatic fragen:
Erstellen Sie einen vollständigen Tilgungsplan für meinen 400.000 $-Kredit.
Excelmatic kann eine vollständige Tabelle erstellen, die die Aufschlüsselung von Tilgung und Zinsen für jede einzelne Zahlung über die Laufzeit des Kredits hinweg zeigt, eine Aufgabe, die manuell in Excel erhebliche Zeit in Anspruch nehmen würde.
Traditionelle Formeln vs. KI: Ein schneller Vergleich
| Merkmal | Traditionelle PMT()-Funktion |
Excelmatic (KI-Agent) |
|---|---|---|
| Lernkurve | Steil: Erfordert das Auswendiglernen von Syntax, Parametern und Regeln. | Minimal: Verwendet einfache Sprache. |
| Geschwindigkeit | Manuell: Erfordert das Eingeben von Formeln und das Anpassen von Parametern. | Sofort: Stellt eine Frage, erhält eine Antwort. |
| Fehleranfälligkeit | Hoch: Anfällig für Syntaxfehler, Vorzeichenfehler und Häufigkeitsfehler. | Niedrig: Interpretiert die Benutzerabsicht und vermeidet häufige Formelfehler. |
| Flexibilität | Mäßig: Erfordert die Kombination mehrerer Funktionen für tiefgreifendere Analysen. | Hoch: Kann Folge- und erweiterte Fragen beantworten und vollständige Berichte oder Diagramme erstellen. |
| Erweiterte Analyse | Komplex: Die Erstellung eines Tilgungsplans oder einer Szenarioanalyse ist manuell. | Einfach: Kann komplexe Berichte aus einer einzigen Eingabe generieren. |
Fazit
Ob Sie ein Finanzanalyst, ein Kleinunternehmer sind oder nur Ihre persönlichen Finanzen planen, das Verständnis, wie Kredit- und Investitionszahlungen berechnet werden, ist unerlässlich. Der traditionelle Weg der Beherrschung von Excels PMT()-Funktion und ihren Gegenstücken bietet ein solides, grundlegendes Verständnis.
Allerdings geht es bei der Zukunft der Datenanalyse um Effizienz und Zugänglichkeit. KI-gestützte Tools wie Excelmatic sind nicht nur eine Abkürzung; sie sind eine intelligentere Art zu arbeiten. Sie befähigen Sie, sich auf die Finanzfragen zu konzentrieren, die Sie beantworten möchten, und nicht auf die komplexe Syntax, die benötigt wird, um sie zu stellen. Indem sie die Berechnungen, Anpassungen und sogar die Erstellung umfassender Berichte übernehmen, lassen diese Tools Sie in Rekordzeit von Daten zu Entscheidungen gelangen.
Bereit, Ihre Finanzanalyse zu optimieren und sofortige Zahlungsberechnungen zu erhalten? Testen Sie Excelmatic noch heute und entdecken Sie, wie einfach es ist, mit KI intelligentere Finanzentscheidungen zu treffen.
FAQ
Was ist die PMT()-Funktion in Excel?
Die PMT()-Funktion in Excel berechnet die Zahlung für einen Kredit basierend auf konstanten Zahlungen und einem konstanten Zinssatz. Sie wird häufig für Hypotheken, Autokredite und Investitionsberechnungen verwendet.
Wann sollte ich die PMT-Funktion anstelle eines KI-Tools verwenden?
Die manuelle Verwendung der PMT()-Funktion ist ideal, um die Mechanik von Finanzberechnungen zu erlernen oder um hochgradig angepasste, überprüfbare Finanzmodelle zu erstellen, bei denen jeder Schritt in einer Formel sichtbar sein muss. Für schnelle Antworten, Berichterstattung und die Vermeidung manueller Fehler ist ein KI-Tool wie Excelmatic oft effizienter.
Warum gibt meine PMT()-Funktion eine negative Zahl zurück?
Die PMT()-Funktion folgt Excels Cashflow-Konvention, bei der ausgehende Zahlungen als negative Zahlen erscheinen. Wenn Sie die Zahlung als positive Zahl anzeigen möchten, fügen Sie einfach ein negatives Vorzeichen vor Ihrer PMT-Formel hinzu (z.B. =-PMT(...)). KI-Tools wie Excelmatic stellen dies oft intuitiver dar, indem sie den Zahlungsbetrag direkt angeben.
Was ist der Unterschied zwischen PMT-, IPMT- und PPMT()-Funktionen?
PMT() berechnet den Gesamtzahlungsbetrag, IPMT() berechnet nur den Zinsanteil einer bestimmten Zahlung und PPMT() berechnet nur den Tilgungsanteil. Für jede gegebene Periode wird IPMT + PPMT immer gleich PMT sein.
Wie berücksichtige ich eine anfängliche Anzahlung in meiner Berechnung?
Mit der PMT()-Funktion subtrahieren Sie die Anzahlung vom Gesamtpreis, bevor Sie ihn als Barwert (pv) eingeben. Zum Beispiel, für ein 350.000 $-Haus mit einer 50.000 $-Anzahlung ist Ihr pv 300.000 $. Mit einem KI-Tool wie Excelmatic können Sie dies oft direkt angeben, wie z.B. "Berechnen Sie die Zahlungen für ein 350.000 $-Haus mit einer 50.000 $-Anzahlung", und es erledigt die Mathematik für Sie.