Eine Anleitung zur NORM.VERT-Funktion in Excel - Formeln vs. KI

Wenn Sie häufig mit Wahrscheinlichkeiten und Statistiken in Excel arbeiten, werden Sie unweigerlich Normalverteilungen analysieren müssen – sei es bei der Qualitätskontrolle, der Bewertung von Testergebnissen oder der Auswertung von Geschäftsdaten. Traditionell bedeutete dies, Funktionen wie NORM.DIST() zu beherrschen, um die Wahrscheinlichkeit für einen bestimmten Wert zu bestimmen.

Aber heute haben Sie mehr als eine Möglichkeit, die Aufgabe zu erledigen. Während der klassische formelbasierte Ansatz Präzision und Kontrolle bietet, bieten moderne KI-Tools einen schnelleren, intuitiveren Weg zu denselben Antworten.

In diesem Leitfaden werden wir beide Methoden untersuchen. Wir werden die traditionelle NORM.DIST()-Funktion, ihre Syntax und ihre Optionen aufschlüsseln. Dann stellen wir eine leistungsstarke, KI-gestützte Alternative vor, Excelmatic, um Ihnen zu zeigen, wie Sie dieselben Ergebnisse einfach durch Stellen einer Frage erhalten. Am Ende haben Sie ein vollständiges Bild davon, wie Sie Normalverteilungsanalysen in Excel durchführen können, und können die Methode wählen, die am besten zu Ihrem Workflow passt.

Was ist eine Normalverteilungsberechnung?

Bevor wir uns mit dem "Wie" befassen, klären wir das "Was". Eine Normalverteilungsberechnung hilft Ihnen, die Wahrscheinlichkeit zu finden, dass ein Wert, der aus einem glockenförmigen Datensatz gezogen wird, kleiner oder gleich einer bestimmten Zahl ist. Je nach Bedarf können Sie entweder die kumulative Wahrscheinlichkeit (die Fläche unter der Kurve bis zu einem Punkt) oder die Wahrscheinlichkeitsdichte (die Höhe der Kurve an diesem bestimmten Punkt) erhalten.

Egal, ob Sie herausfinden möchten, wie wahrscheinlich es ist, unter einer bestimmten Punktzahl zu liegen, oder einfach den Wert der Normalverteilungskurve an einem Punkt benötigen – beide Methoden, die traditionelle und die KI-Methode, bieten eine Lösung.

Methode 1: Der traditionelle Formelansatz mit NORM.DIST()

Für Anwender, die mit Excel-Formeln vertraut sind, ist NORM.DIST() die go-to-Funktion für diese Aufgabe. Sehen wir uns an, wie man sie verwendet.

NORM.DIST()-Syntax und Argumente

Hier ist die Syntax der Funktion:

=NORM.DIST(x, mean, standard_dev, cumulative)

Aufschlüsselung der einzelnen Argumente:

• x: Der Wert, für den Sie die Verteilung wünschen.
• mean: Der Mittelwert (Durchschnitt) der Verteilung.
• standard_dev: Die Standardabweichung der Verteilung.
• cumulative: Ein logischer Wert – verwenden Sie TRUE für die kumulative Verteilungsfunktion (CDF) oder FALSE für die Wahrscheinlichkeitsdichtefunktion (PDF).

Um dies in einen Kontext zu setzen: Stellen Sie sich vor, Sie möchten die Wahrscheinlichkeit finden, dass ein Wert kleiner oder gleich 80 in einer Normalverteilung mit einem Mittelwert von 70 und einer Standardabweichung von 10 ist. Die Formel würde so aussehen:

=NORM.DIST(80, 70, 10, TRUE)

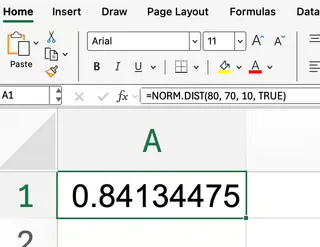
Dieser Aufbau gibt die kumulative Wahrscheinlichkeit bis zu 80 zurück.

Kumulativ vs. Wahrscheinlichkeitsdichte

Das Verständnis des cumulative-Arguments ist entscheidend, um die gewünschten Ergebnisse zu erhalten.

• Kumulativ (TRUE): Wenn Sie das letzte Argument auf TRUE setzen, gibt NORM.DIST() die Wahrscheinlichkeit zurück, dass ein Wert kleiner oder gleich x ist. Dies ist die gebräuchlichste Option für die statistische Analyse, da sie Fragen wie "Wie viel Prozent der Schüler haben 85 oder weniger erreicht?" beantwortet.
• Wahrscheinlichkeitsdichte (FALSE): Wenn Sie FALSE wählen, gibt die Funktion die Höhe der Normalverteilungskurve bei x an. Dies ist keine Wahrscheinlichkeit an sich, aber nützlich für die statistische Modellierung oder zum Zeichnen der Verteilungskurve.

Methode 2: Der moderne KI-Ansatz mit Excelmatic

Was wäre, wenn Sie die Syntax überspringen und einfach nach dem fragen könnten, was Sie brauchen? Hier kommt Excelmatic ins Spiel. Als Excel-KI-Agent übersetzt es Klartext-Anfragen in sofortige Antworten, Diagramme und Erkenntnisse.

Anstatt sich die NORM.DIST-Funktion und ihre vier Argumente zu merken, können Sie Ihre Anfrage einfach formulieren. Für das gleiche Szenario wie oben (Mittelwert=70, Standardabweichung=10, Wert=80) würden Sie Excelmatic sagen:

Was ist die kumulative Wahrscheinlichkeit für einen Wert von 80 in einer Normalverteilung mit einem Mittelwert von 70 und einer Standardabweichung von 10?

Excelmatic verarbeitet diese Anfrage und liefert die Antwort direkt, ohne dass Sie jemals eine Formel eingeben müssen. Dieser Ansatz ist nicht nur schneller, sondern auch weniger anfällig für Fehler, die durch falsche Syntax oder falsche Argumentreihenfolge verursacht werden.

Praktische Beispiele: Ein direkter Vergleich

Lassen Sie uns beide Methoden in Aktion sehen, um reale Probleme zu lösen.

1. Ermitteln der kumulativen Wahrscheinlichkeit

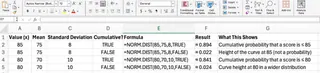
Angenommen, Sie möchten die Wahrscheinlichkeit wissen, dass ein Testergebnis kleiner oder gleich 85 ist, wobei davon ausgegangen wird, dass die Testergebnisse normalverteilt sind mit einem Mittelwert von 75 und einer Standardabweichung von 8.

Traditionelle NORM.DIST()-Methode:

Sie würden die folgende Formel in eine Zelle eingeben:

=NORM.DIST(85, 75, 8, TRUE)

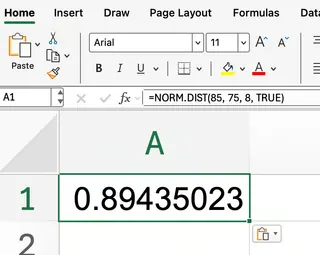
Excel gibt einen Wert nahe 0,894 zurück, was bedeutet, dass etwa 89,4 % der Schüler 85 oder weniger erreicht haben.

Excelmatic KI-Methode:

Sie würden einfach fragen:

Wie hoch ist die Wahrscheinlichkeit, dass ein Testergebnis 85 oder niedriger ist, wenn die Ergebnisse normalverteilt sind mit einem Mittelwert von 75 und einer Standardabweichung von 8?

Excelmatic liefert sofort die gleiche Antwort, 0,894, und spart Ihnen die Zeit und Mühe, die Formel zu konstruieren.

2. Erhalten der Wahrscheinlichkeitsdichte

Was wäre nun, wenn Sie an der Höhe der Kurve an einem bestimmten Wert interessiert wären, und nicht an der kumulativen Wahrscheinlichkeit?

Traditionelle NORM.DIST()-Methode:

Hier setzen Sie das cumulative-Argument auf FALSE:

=NORM.DIST(85, 75, 8, FALSE)

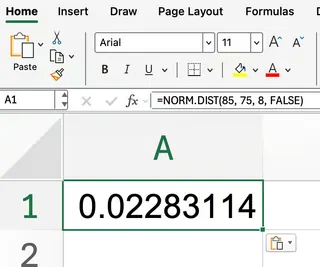
Dies gibt Ihnen die Wahrscheinlichkeitsdichte bei 85. Denken Sie daran, dass dies keine Wahrscheinlichkeit ist, sondern der Wert der Normalverteilungskurve an diesem Punkt.

Excelmatic KI-Methode:

Ihre Anfrage wäre ebenso unkompliziert:

Berechne die Wahrscheinlichkeitsdichte bei einem Wert von 85 für eine Normalverteilung mit einem Mittelwert von 75 und einer Standardabweichung von 8.

Wieder übernimmt Excelmatic die Berechnung im Hintergrund und gibt den korrekten Wert zurück. Die folgende Tabelle fasst zusammen, wie sich die Eingaben auf die Ausgabe für beide Modi auswirken.

Visualisierung der Normalverteilung

Die Visualisierung der Glockenkurve ist eine großartige Möglichkeit, die Verteilung zu verstehen. Auch hier bietet der KI-Ansatz eine erhebliche Abkürzung.

Traditionelle Methode: Manuelle Diagrammerstellung

Um ein Diagramm in Excel zu erstellen, müssen Sie zunächst die Datenpunkte manuell generieren:

1. Erstellen Sie eine Spalte mit x-Werten (z. B. von 60 bis 90 in Schritten von 1).
2. Erstellen Sie eine zweite Spalte für die kumulativen Werte mit der Formel: =NORM.DIST(x_cell, 75, 8, TRUE).
3. Erstellen Sie eine dritte Spalte für die Wahrscheinlichkeitsdichte-Werte: =NORM.DIST(x_cell, 75, 8, FALSE).
4. Markieren Sie alle drei Spalten.
5. Gehen Sie zu Einfügen > Diagramme > Liniendiagramm oder Punkt (XY) mit geglätteten Linien, um Ihre Visualisierung zu erstellen.

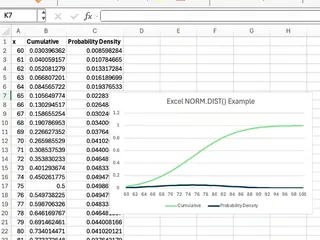
Obwohl effektiv, ist dieser Prozess mehrstufig und zeitaufwändig.

Excelmatic-Methode: Sofortige Diagrammgenerierung

Mit Excelmatic können Sie die manuelle Datenvorbereitung und Diagrammformatierung umgehen. Fragen Sie einfach:

Erstelle ein Liniendiagramm, das die kumulativen und Wahrscheinlichkeitsdichte-Kurven für eine Normalverteilung mit einem Mittelwert von 75 und einer Standardabweichung von 8 zeigt. Verwende x-Werte von 60 bis 90.

Excelmatic generiert die Daten und das Diagramm für Sie in einem Schritt und liefert die gleiche professionell aussehende Visualisierung in einem Bruchteil der Zeit.

Häufige Probleme und Tipps für die NORM.DIST()-Funktion

Wenn Sie den traditionellen Formelweg wählen, sollten Sie sich einiger häufiger Fallstricke bewusst sein:

• Standardabweichung muss positiv sein. Die Eingabe von Null oder einer negativen Zahl führt zu einem #NUM!-Fehler.
• Flexibilität von Mittelwert und Standardabweichung. Der Mittelwert kann eine beliebige reelle Zahl sein, aber die Standardabweichung muss immer positiv sein.
• Umgekehrter Weg? Wenn Sie eine Wahrscheinlichkeit haben und den entsprechenden Wert finden müssen, verwenden Sie stattdessen die NORM.INV()-Funktion.

Verwandte Funktionen in Excel

Die NORM.DIST()-Familie umfasst mehrere andere nützliche Funktionen für die statistische Analyse:

• NORM.INV(): Die Umkehrung von NORM.DIST(), gibt den Wert für eine gegebene kumulative Wahrscheinlichkeit zurück.
• NORM.S.DIST(): Berechnet Wahrscheinlichkeiten für die Standardnormalverteilung (Mittelwert=0, Standardabweichung=1).
• NORM.S.INV(): Gibt den Wert für eine gegebene Wahrscheinlichkeit in der Standardnormalverteilung zurück.

Während Sie die Syntax für jede Funktion lernen können, denken Sie daran, dass ein KI-Tool wie Excelmatic diese Aufgaben ebenfalls durch einfache, konversationsbasierte Anfragen erledigen kann (z. B. "Welcher Wert entspricht unter Verwendung einer Standardnormalverteilung einer kumulativen Wahrscheinlichkeit von 0,95?").

Fazit

Sie haben nun gesehen, wie Sie Normalverteilungsanalysen in Excel mit zwei verschiedenen, aber gleichermaßen leistungsstarken Methoden angehen können. Die traditionelle NORM.DIST()-Funktion bietet granulare Kontrolle und ist eine grundlegende Fähigkeit für jeden ernsthaften Excel-Anwender. Gleichzeitig revolutionieren KI-Agenten wie Excelmatic die Datenanalyse, indem sie komplexe statistische Aufgaben schneller, einfacher und für alle zugänglicher machen.

Ihre Wahl der Methode hängt von Ihren Bedürfnissen ab. Wenn Sie komplexe, vernetzte Dashboards erstellen, sind Formeln vielleicht der richtige Weg. Aber für schnelle Analysen, Visualisierungen und um sofortige Antworten zu erhalten, ohne sich in der Syntax zu verlieren, ist der KI-Ansatz ein klarer Gewinner.

Bereit, Ihre statistische Analyse zu vereinfachen? Hören Sie auf, Formeln auswendig zu lernen, und fangen Sie an, Fragen zu stellen. Testen Sie Excelmatic noch heute und erhalten Sie die Wahrscheinlichkeiten und Erkenntnisse, die Sie sofort benötigen.