Wichtige Erkenntnisse
- Manuelle Schiefe-Berechnungen in Excel erfordern technisches Wissen über Funktionen wie
SKEW()oder komplexe Data Analysis ToolPak-Einrichtung - Excelmatic bietet sofortige Schiefe-Analyse mit einfacher Sprache - keine Formeln oder statistische Kenntnisse erforderlich
- Das Verständnis der Datenschiefe hilft bei der Identifizierung von Geschäftseinblicken wie Kundenzwartezeitmustern oder Vertriebsverteilungsanomalien
- KI-gestützte Analyse spart Zeit und reduziert Fehler für Marketing-, Vertriebs- und Betriebsmitarbeiter, die schnelle Dateneinblicke benötigen
Das Verständnis der Schiefe Ihrer Daten ist ein entscheidender Schritt in jedem Analyseprojekt. Es hilft, potenzielle Ausreißer oder Anomalien zu identifizieren, die auf Datenqualitätsprobleme oder Bereiche hinweisen könnten, die weitere Untersuchungen erfordern. Die Schiefe liefert auch Einblicke in die Asymmetrie der Daten, was die Wahl der statistischen Methoden und nachgelagerten Modelle beeinflusst.
In diesem Tutorial behandeln wir das Konzept der Schiefe, ihre mathematischen Definitionen und die verschiedenen Arten von Schiefe in Datenverteilungen. Anhand eines einfachen Praxisbeispiels berechnen wir die Schiefe mit traditionellen Microsoft Excel-Methoden und vergleichen sie mit einem modernen, KI-gestützten Ansatz. Wenn Sie am Ende dieses Tutorials Ihre Fähigkeiten weiter ausbauen möchten, sollten Sie unseren Kurs Datenanalyse in Excel in Betracht ziehen.
Die kurze Antwort: So berechnen Sie Schiefe in Excel
Um schnell Schiefe in Excel zu berechnen, verwenden Sie entweder die Funktion SKEW() für eine Stichprobe oder die Funktion SKEW.P() für eine gesamte Grundgesamtheit.
Folgen Sie diesen Schritten:
- Geben Sie Ihre Daten in eine einzelne Spalte ein.
- Tippen Sie in eine neue Zelle
=SKEW(Bereich)oder=SKEW.P(Bereich), wobeiBereichder Zellbereich Ihrer Daten ist. - Drücken Sie Eingabe, um den Schiefewert zu erhalten. Die Schiefe wird durch eine einzelne Zahl dargestellt.
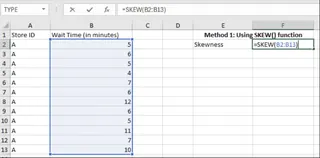
Berechnung der Schiefe mit der SKEW()-Funktion. Bild vom Autor
Während dies die schnellste manuelle Methode ist, können KI-gestützte Tools diese Analyse jetzt noch intuitiver durchführen, einfach indem Sie eine Frage in einfacher Sprache stellen. Dies werden wir später in dieser Anleitung untersuchen.
Was ist Schiefe?
Schiefe ist eine statistische Metrik, die die Asymmetrie einer Verteilung misst. Sie gibt an, ob die Datenpunkte tendenziell mehr auf einer Seite des Mittelwerts fallen als auf der anderen.
Sie gilt als das dritte Moment einer Verteilung:
- Mittelwert (Erstes Moment): Der Durchschnitt der Daten, der einen Maßstab für den typischen Wert liefert.
- Streuung (Zweites Moment): Die Variabilität der Daten, die quantifiziert, wie sehr Datenpunkte vom Mittelwert abweichen.
- Schiefe (Drittes Moment): Die Asymmetrie der Datenverteilung um ihren Mittelwert.
- Kurtosis (Viertes Moment): Die "Schwanzlastigkeit" oder Spitzigkeit der Datenverteilung, die Einblicke in das Gewicht der Schwänze gibt.
Schiefe Verteilungen
Abhängig davon, ob der Schiefekoeffizient positiv, negativ oder null ist, gibt es drei Arten von Schiefe.
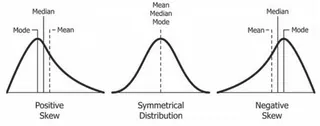
Schiefe Verteilungen. Quelle: Wikipedia
- Positive Schiefe (Rechtsschiefe): Der Schwanz auf der rechten Seite der Verteilung ist länger als der linke. Die meisten Datenpunkte konzentrieren sich links. Der Mittelwert ist typischerweise größer als der Median.
- Null Schiefe (Symmetrische Verteilung): Die Verteilung ist perfekt symmetrisch. Die Schwänze auf beiden Seiten sind ausgeglichen, und Mittelwert und Median sind gleich.
- Negative Schiefe (Linksschiefe): Der Schwanz auf der linken Seite der Verteilung ist länger als der rechte. Datenpunkte konzentrieren sich rechts. Der Mittelwert ist typischerweise kleiner als der Median.
Während sich die Schiefe auf die Streuung (Schwänze) der Verteilung konzentriert, konzentriert sich eine andere statistische Metrik, die Kurtosis, mehr auf die Höhe und Spitzigkeit. Mit KI-Tools wie Excelmatic können Sie sowohl Schiefe als auch Kurtosis in einer einzigen Abfrage einfach berechnen und so ein vollständiges Bild Ihrer Datenverteilung erhalten, ohne mehrere statistische Funktionen erlernen zu müssen.
Nachdem wir das Konzept verstanden haben, berechnen wir es nun für Beispieldaten mit Excel.
Methoden zur Berechnung der Schiefe in Excel
Stellen Sie sich vor, Sie sind ein Datenanalyst, der damit beauftragt ist, die Wartezeiten der Kunden in einer beliebten Einzelhandelskette zu analysieren. Die Geschäftsleitung vermutet, dass lange Wartezeiten zu unterschiedlichen Kundenzufriedenheitsniveaus beitragen könnten. Zur Untersuchung haben sie Stichprobendaten zu Kundenwartezeiten aus einem Geschäft über einige Tage gesammelt.
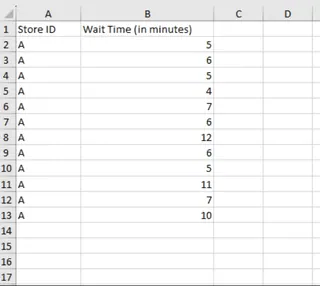
Kundenwartezeit-Datensatz. Bild vom Autor
Hier sind drei Methoden, die Sie verwenden könnten, um die Schiefe-Metrik für diese Daten zu berechnen.
Methode 1: Verwendung der SKEW()-Funktion
Der direkteste Weg, die Stichprobenschiefe zu berechnen, ist mit Excels integrierter SKEW()-Funktion.
Die Syntax ist einfach:
SKEW(Zahl1; [Zahl2]; ...)
Sie können bis zu 255 Argumente eingeben, die einzelne Zahlen oder einen Zellbereich sein können.
Für unsere Daten würden wir die folgende Formel in eine Zelle eingeben, z. B. F2:
=SKEW(B2:B13)
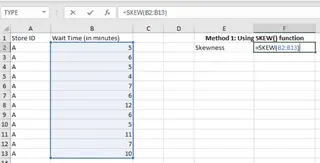
Berechnung der Schiefe mit der SKEW()-Funktion. Bild vom Autor
Das Drücken von Eingabe liefert uns den Schiefekoeffizienten.
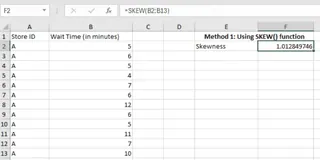 Schiefe-Ergebnis. Bild vom Autor
Schiefe-Ergebnis. Bild vom Autor
Der positive Ausgabewert zeigt an, dass die Wartezeiten rechtsschief sind. Bevor wir dies interpretieren, wollen wir eine andere Methode untersuchen.
Methode 2: Verwendung des Data Analysis ToolPak
Für eine umfassendere statistische Zusammenfassung können Sie den Data Analysis Toolpak verwenden, ein Excel-Add-In.
Wenn Sie es nicht aktiviert haben, müssen Sie es zuerst einrichten. Gehen Sie zu Datei > Optionen > Add-Ins. Wählen Sie im Feld Verwalten die Option Excel-Add-Ins und klicken Sie auf Gehe zu. Aktivieren Sie das Kontrollkästchen Analyse-Funktionen und klicken Sie auf OK.
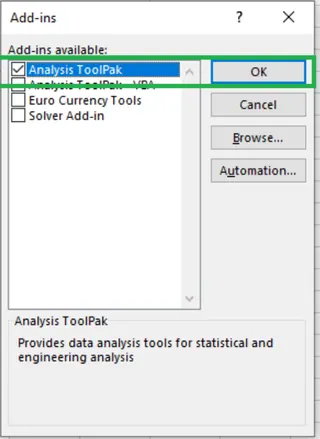 Aktivieren des Data Analysis ToolPak. Bild vom Autor
Aktivieren des Data Analysis ToolPak. Bild vom Autor
Sobald aktiviert, erscheint das Symbol Datenanalyse unter dem Tab Daten.
Klicken Sie auf das Symbol Datenanalyse im Tab Daten.
Wählen Sie Deskriptive Statistik aus der Liste aus und klicken Sie auf OK.
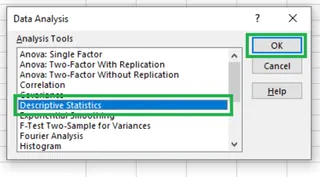 Auswahl der deskriptiven Statistik. Bild vom Autor
Auswahl der deskriptiven Statistik. Bild vom AutorIm Dialogfeld:
- Setzen Sie den Eingabebereich auf Ihre Daten (
$B$1:$B$13). - Aktivieren Sie Beschriftungen in erster Zeile, da unsere Auswahl die Kopfzeile enthält.
- Wählen Sie einen Ausgabebereich (z. B. Zelle
$E$5). - Aktivieren Sie Übersichtsstatistiken.
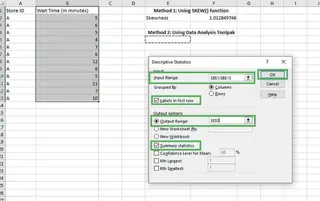 Ausfüllen der Details für deskriptive Statistik. Bild vom Autor
Ausfüllen der Details für deskriptive Statistik. Bild vom Autor- Setzen Sie den Eingabebereich auf Ihre Daten (
Klicken Sie auf OK. Excel generiert eine vollständige Tabelle mit deskriptiven Statistiken, einschließlich der Schiefe.
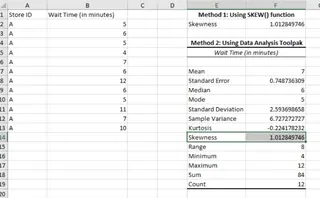 Ergebnisse der deskriptiven Statistik. Bild vom Autor
Ergebnisse der deskriptiven Statistik. Bild vom Autor
Diese Methode ist leistungsstark, da sie die Schiefe zusammen mit anderen wichtigen Metriken wie Mittelwert, Median, Modus und Standardabweichung auf einen Schlag liefert.
Methode 3: Der KI-gestützte Weg mit Excelmatic
Für Geschäftsanwender, die schnelle Einblicke ohne technische Hürden benötigen, bieten KI-Tools wie Excelmatic einen revolutionären Ansatz. Excelmatic ist ein KI-Excel-Agent, der sofortige Antworten und Einblicke aus Ihren Daten liefert, ohne dass Sie sich Formeln merken oder Menüs navigieren müssen.
Anstatt Formeln oder mehrstufige Einrichtungen verwenden Sie einfach einfache Sprache, um das zu fragen, was Sie benötigen.
So würden Sie die Schiefe mit Excelmatic berechnen:
- Laden Sie Ihre Datei hoch: Laden Sie sicher Ihre Excel-Tabelle mit den Kundenwartezeiten hoch.
Stellen Sie Ihre Frage: Tippen Sie im Chat-Interface einfach Ihre Anfrage ein, wie z. B.:
"Berechne die Schiefe für die Spalte 'Wartezeit (Minuten)'."
Oder für eine breitere Analyse:
"Gib mir eine deskriptive Statistik-Zusammenfassung für die Kundenwartezeiten."

- Erhalten Sie sofortige Ergebnisse: Excelmatic verarbeitet Ihre Anfrage und liefert sofort den Schiefewert zusammen mit anderen relevanten Statistiken, genau wie der Data Analysis ToolPak, aber ohne jegliche Einrichtung. Es könnte Ihnen auch anbieten, die Verteilung für Sie zu visualisieren.

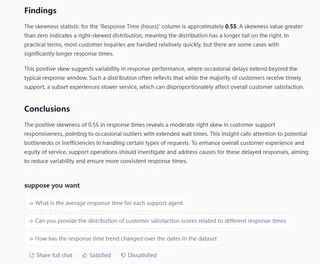
Dieser Ansatz umgeht vollständig die Notwendigkeit, Add-Ins zu aktivieren oder Funktionssyntax auswendig zu lernen, und macht komplexe Analysen für jeden zugänglich.
Vergleich der Methoden
| Merkmal | SKEW()-Funktion | Data Analysis ToolPak | Excelmatic (KI-Agent) |
|---|---|---|---|
| Benutzerfreundlichkeit | Einfach, wenn Sie die Funktion kennen. | Mittel, erfordert einmalige Einrichtung und Menünavigation. | Sehr einfach, verwendet natürliche Sprache. |
| Geschwindigkeit | Schnell für eine einzelne Berechnung. | Langsamer aufgrund mehrerer Schritte. | Sofort. |
| Erforderliches Wissen | Kenntnis von Excel-Funktionen (SKEW). |
Kenntnis von Excel-Add-Ins und statistischen Begriffen. | Keine spezifischen Excel-Kenntnisse erforderlich. |
| Umfang der Analyse | Berechnet nur Schiefe. | Bietet eine vollständige Zusammenfassung der deskriptiven Statistik. | Bietet vollständige Zusammenfassung + Diagramme + Einblicke. |
Interpretation der Schiefe-Ergebnisse
Mit allen drei Methoden erhalten wir denselben Schiefewert von 1,0128 für die Kundenwartezeiten. Das sagt uns Folgendes:
- Rechtsschiefe Verteilung: Der positive Wert zeigt eine rechtsschiefe (positiv schiefe) Verteilung an. Das bedeutet, dass die meisten Wartezeiten kurz sind, es aber Ausreißer mit ungewöhnlich hohen Wartezeiten gibt.
- Mittelwert versus Median: Die durchschnittliche Wartezeit (5,83 Min.) ist höher als der Median (5,5 Min.). Dies bestätigt, dass einige deutlich längere Wartezeiten den Durchschnitt nach oben ziehen. Der Median ist wahrscheinlich das bessere Maß für das typische Kundenerlebnis.
- Geschäftseinblicke: Der Modus beträgt 5 Minuten, die häufigste Wartezeit. Die Rechtsschiefe zeigt jedoch Inkonsistenzen auf. Die Geschäftsleitung sollte sich darauf konzentrieren, die Ursachen dieser langen Wartezeit-Ausreißer zu verstehen und zu reduzieren, um die allgemeine Kundenzufriedenheit zu verbessern.
Wenn die Schiefe negativ wäre, würde dies auf eine linksschiefe Verteilung hindeuten, was darauf hindeutet, dass die meisten Kunden längere Wartezeiten erleben, mit einigen Ausreißern mit außergewöhnlich kurzen Wartezeiten.
Ein tieferer Einblick: Was die Excel-Schiefe-Funktionen tun
Excels Schiefe-Funktionen berechnen die momentbasierte Schiefe, das dritte standardisierte Moment. Sie quantifiziert die Asymmetrie, indem sie die kubischen Abweichungen vom Mittelwert mit der kubischen Standardabweichung vergleicht.
Für eine Datenstichprobe lautet die verwendete Formel:
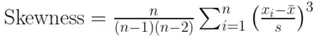
Momentbasierte Schiefe-Gleichung. Bild vom Autor
Wo:
- n die Anzahl der Datenpunkte ist.
- Xi jeder einzelne Datenpunkt ist.
- x̄ der Mittelwert der Datenpunkte ist.
- s die Stichprobenstandardabweichung ist.
Die SKEW()-Funktion verwendet diese Formel, die einen Korrekturfaktor (n / ((n-1)*(n-2))) enthält, um eine unverzerrte Schätzung für eine Stichprobe zu liefern. Die SKEW.P()-Funktion berechnet die Schiefe für eine gesamte Grundgesamtheit und verwendet eine einfachere Formel ohne diese Korrektur.
Weiterführende Literatur: Andere Arten von Schiefe
Während die momentbasierte Schiefe am gebräuchlichsten ist, existieren andere Maße:
- Pearsons Schiefekoeffizienten: Verwenden Mittelwert, Modus und Median. Der zweite Koeffizient (unter Verwendung des Medians) ist robuster gegenüber Ausreißern.
- Kellys Schiefemaß: Basierend auf Perzentilen (P10, P50, P90), konzentriert sich auf die Schwänze der Verteilung.
- Bowleys Schiefemaß: Basierend auf Quartilen (Q1, Q2, Q3), was es hochgradig resistent gegenüber Extremwerten macht.
 Bowleys Schiefe-Gleichung. Bild vom Autor
Bowleys Schiefe-Gleichung. Bild vom Autor
Abschließende Gedanken
Dieses Tutorial hat Sie in das Konzept der Schiefe eingeführt und gezeigt, wie man sie in Excel berechnet. Wir haben die traditionelle SKEW()-Funktion und den umfassenden Data Analysis ToolPak behandelt. Wir haben auch untersucht, wie moderne KI-Tools wie Excelmatic diesen Prozess revolutionieren, indem sie Ihnen die gleichen, wenn nicht besseren, Einblicke ermöglichen, indem Sie einfach eine Frage stellen.
Ihr Lernen muss hier nicht aufhören. Excelmatic bietet umfassende Ressourcen, um Ihre Datenkompetenzen ohne die technische Komplexität zu verbessern: unsere vereinfachten Statistik-Tutorials brechen Konzepte wie Schiefe in praktische Geschäftsanwendungen herunter, unsere Excel-Grundlagen-Anleitungen helfen Ihnen, wesentliche Datenoperationen durch intuitive Beispiele zu meistern






