Key Takeaways:
- Calculating standard deviation is key for assessing volatility in business metrics like sales and traffic, but traditional Excel methods require memorizing complex functions and statistical concepts.
- Excelmatic enables complex calculations like standard deviation through simple language commands, eliminating the need to remember formulas and lowering the technical barrier to data analysis.
- Compared to manual methods, Excelmatic automatically identifies data types and applies the correct formula, while also generating visualizations, significantly boosting efficiency and accuracy.
- For professionals who need to make data-driven decisions, tools like Excelmatic shift the focus from technical implementation to interpreting insights and developing strategy.
Standard deviation tells us how spread out the numbers are in a given dataset. Several important statistical concepts and methods, such as variance, coefficient of variation, and confidence intervals, depend on standard deviation as a foundational measure of variability, thus making it one of the most important tools in statistics for data professionals to master.
This article will introduce you to standard deviation, guide you through calculating it in Excel using both traditional formulas and modern AI tools, explain the differences between the available methods, and demonstrate how to interpret the results to make informed decisions based on your analysis.
Two Ways to Calculate Standard Deviation in Excel
When it comes to calculating standard deviation, you have two primary paths in Excel: the modern, conversational AI approach and the traditional, formula-based method.
The AI-Powered Way: Using Excelmatic
The fastest and most intuitive way to get the job done is with an AI agent like Excelmatic. Instead of memorizing functions and syntax, you simply ask for what you need in plain language.
With Excelmatic, the process is simple:
- Upload your Excel file containing the dataset.
- Ask a direct question, such as:
- "Calculate the standard deviation for the daily sales in column B."
- "What is the sample standard deviation of my sales data?"
- "Show me the variability in daily sales."
Excelmatic handles everything else. It automatically identifies the data, applies the correct statistical formula (population or sample), and delivers the answer instantly. This approach eliminates the need to remember the difference between STDEV.P and STDEV.S or worry about cell ranges, saving you time and reducing the chance of errors.
The Traditional Formula Way: Using Excel Functions
To calculate standard deviation manually in Excel, you use the STDEV.P() function for a population or the STDEV.S() function for a sample.

For example, if your data is in cells B2 to B31, you would type =STDEV.P(B2:B31) to calculate the population standard deviation or =STDEV.S(B2:B31) for the sample standard deviation. Excel will then compute and display the result. While effective, this method requires you to know which function is appropriate for your data.
What is Standard Deviation?
Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of numerical values. It indicates how much the values in a dataset deviate from the mean (average) of the dataset.
It helps to understand the extent of variability within data—a low standard deviation indicates that the values are close to the mean, suggesting consistency, while a high standard deviation indicates greater variability, suggesting more spread-out data.
Formulas for standard deviation
The formula for standard deviation depends on whether we are dealing with a population or a sample. The formula for population standard deviation (σ) is as follows:
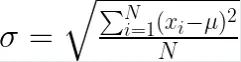
Where:
Nis the total number of data points in the population.x_i represents each individual data point.μis the mean (average) of the population.
This formula calculates the average of the squared deviations from the mean and then takes the square root of this average.
The formula for sample standard deviation (s) is as follows. Note that for sample standard deviation, we use a lowercase n for convention.
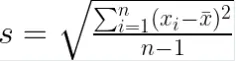
Where:
nis the total number of data points in the sample.x_i represents each individual data point.xˉis the mean (average) of the sample.
The formula is similar to that of the population standard deviation. Still, it uses n - 1 (Bessel’s correction) in the denominator to account for the fact that a sample is being used to estimate the population parameter. This correction makes the sample standard deviation an unbiased estimator of the population standard deviation.
Practical applications of standard deviation
Standard deviation is a commonly used technique across fields. It provides valuable insights into data variability and consistency and can be applied across domains, including:
- Risk Assessment: Standard deviation can measure the volatility of asset returns. A higher standard deviation indicates greater risk and potential return variability.
- Quality Control: Manufacturing industries use standard deviation to monitor and control the quality of products, ensuring consistency and adherence to standards.
- Healthcare and Medicine: Standard deviation is used to understand the spread of data such as patient blood pressure or cholesterol levels, helping to identify outliers and normal ranges.
- Education & Research: Standard deviation helps determine the distribution of test scores and evaluate the effectiveness of educational interventions.
- Weather and Climate Studies: Meteorologists use standard deviation to analyze weather data, such as temperature and precipitation, to understand climate variability.
Types of Standard Deviation Functions in Excel
Microsoft Excel has two different functions to calculate standard deviation, depending on whether you are working with an entire population or a sample.
STDEV.P() for population standard deviation
The STDEV.P() function in Excel calculates the standard deviation for an entire population. This function assumes that the provided arguments include the entire population. The syntax for the STDEV.P() function is as follows:
STDEV.P(number1, [number2], ...)
The parameters are:
number1: The first number argument corresponds to a population.[number2], ...: Optional additional numbers or references that correspond to a population, up to 254 arguments.
You should use STDEV.P() when your data represents the entire population of interest, for example, the test scores of all students in a specific school.
STDEV.S() for sample standard deviation
The STDEV.S() function in Excel calculates the standard deviation for a sample of the population. This function assumes that the provided arguments are a sample of the population, not the entire population. The syntax for the STDEV.S() function is as follows:
STDEV.S(number1, [number2], ...)
The parameters are:
number1: The first number argument corresponds to a sample of the population.[number2], ...: Optional additional numbers or references that correspond to a sample, up to 254 arguments.
In practice, when we have a sample of data, we use STDEV.S() to estimate the standard deviation of the entire population. For example, if you are analyzing the test scores of a randomly selected subset of students from a school, STDEV.S() is the appropriate choice.
Calculating Standard Deviation: A Practical Example
Imagine you’re a data analyst tasked with analyzing the sales performance of a small retail store. The owner wants to understand the variability in daily sales over the past month to better manage inventory and staffing.
You have collected the daily sales data for 30 days. Let’s put these records in a column, say B2 to B31, in an Excel spreadsheet.
Let's compare the two methods to find the standard deviation.
Method 1: The Traditional Formula Approach
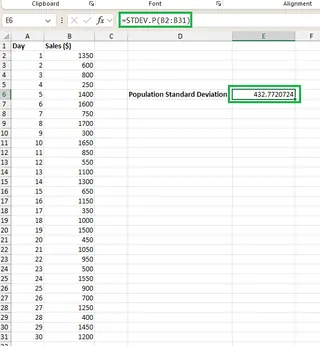
Since our analysis covers the entire month's sales data (our complete population of interest), we use the STDEV.P() function. In cell E6, type the following formula:
=STDEV.P(B2:B31)
Excel calculates the population standard deviation.
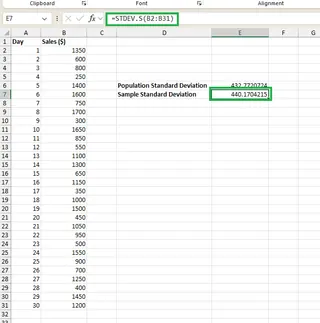
Now, suppose we were using this 30-day data as a sample to estimate performance for the entire year. We would use the STDEV.S() function instead:
=STDEV.S(B2:B31)
This would give us the sample standard deviation.
Method 2: The Excelmatic AI Approach
With Excelmatic, you'd simply upload the spreadsheet and ask:
Calculate the population standard deviation for the data in B2:B31.
Or, if you're treating it as a sample:
What is the sample standard deviation for the daily sales?
Excelmatic provides the answer immediately, without you needing to select a function or input a formula. This is particularly useful when you're unsure which formula to use, as you can describe your goal, and the AI will handle the statistical specifics.
Interpreting Standard Deviation Values
After calculating the standard deviation, the next step is interpreting the result. To do this effectively, it's helpful to also know the mean (average) of the data.
You can calculate this in Excel with =AVERAGE(B2:B31) or by asking Excelmatic, "What is the average of daily sales?".
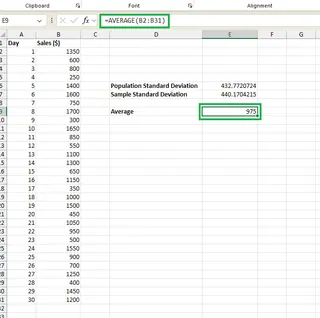
With a mean of $975, we can interpret the standard deviation values:
- Population Standard Deviation (~$432.77): This indicates that, on average, daily sales vary by about $432.77 from the mean of $975. This figure represents the spread of sales data for this specific month.
- Sample Standard Deviation (~$440.17): This value is slightly higher. It's the relevant figure if we’re treating these 30 days as a sample to estimate the variability for a larger period (e.g., the entire year). The higher value accounts for the uncertainty of using a sample.
- High Variability in Sales: Both values indicate high variability. Sales fluctuate significantly from the average, which could impact inventory and staffing. This inconsistency suggests that further analysis might be needed to predict daily sales more accurately.
The store owner should consider this variability when planning to avoid overstocking on slow days or understaffing on busy ones.
How to Add Standard Deviation Bars In Excel
Visualizing variability is powerful. Adding standard deviation bars to a chart in Excel is a great way to do this.
The AI Way: Excelmatic
This is another area where an AI agent shines. Just ask:
Create a line chart of daily sales with standard deviation error bars.
Excelmatic will generate the complete chart for you in a single step.
The Traditional Way: Manual Charting in Excel
- Select your data range (B2 to B31).
- Go to the Insert tab and choose a chart type (e.g., a line chart).
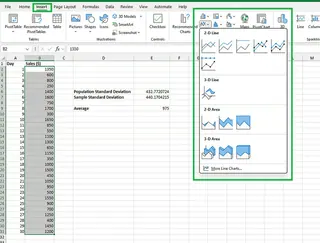
You'll get a simple line chart.
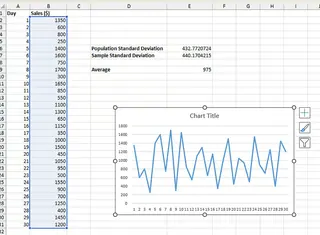
- Click on the chart to bring up the Chart Design tab.
- Click Add Chart Element > Error Bars > Standard Deviation.
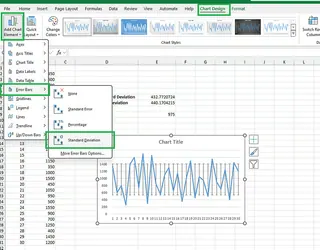
- To customize, you can select More Error Bars Options... to adjust the appearance.
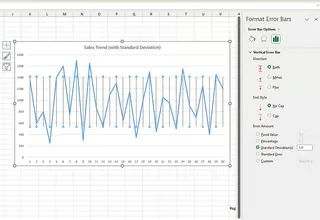
Comparing the two methods, the AI approach is clearly faster and requires no navigation through menus.
Conclusion
Mastering standard deviation is fundamental for robust data analysis, providing critical insight into variability. This guide has demonstrated two distinct approaches within Excel: the foundational precision of built-in functions (STDEV.P, STDEV.S) and the modern efficiency of AI-powered tools.
The evolution from manual formula entry to conversational AI, as exemplified by Excelmatic, represents a significant shift in the data workflow. This transition moves the focus from the technical how of calculation to the strategic why of interpretation. By abstracting complex statistical syntax into simple language commands, AI empowers professionals to execute sophisticated analyses with greater speed, accuracy, and confidence. The ultimate advantage lies not just in obtaining a result faster, but in freeing up cognitive resources for higher-value tasks like insight generation and strategic decision-making.
👉 Experience analyzing Excel data with simple language commands. Start using Excelmatic for free today.
FAQ
When should you use the STDEV.S() function instead of the STDEV.P() function in Excel?
You should use the STDEV.S() function when working with a sample of the population rather than the entire population. Use the STDEV.P() function when your data represents the whole population.
How do you interpret a low standard deviation in a dataset?
A low standard deviation indicates that the values in the dataset are close to the mean, suggesting that the data points are consistently similar to the average value. This implies low variability and high reliability in the data, with fewer deviations from the mean.
Why is standard deviation important in evaluating the accuracy of a regression model?
Standard deviation is important in evaluating the accuracy of a regression model because it quantifies the spread of the residuals (the errors in the model's predictions). By calculating the standard deviation of the residuals, analysts can assess how well the regression model fits the data.
What does a high standard deviation indicate about a dataset?
A high standard deviation indicates that the values in the dataset are spread out over a wider range. This means there is greater variability or dispersion from the mean, suggesting inconsistency in the data, with values deviating significantly from the average.
What is the difference between STDEV.P() and STDEV.S() in Excel?
The main difference between STDEV.P() and STDEV.S() lies in their application and calculation. STDEV.P() is for an entire population and divides by the total number of data points (N). In contrast, STDEV.S() is for a population sample and divides by the number of data points minus one (n-1) to account for sample variability, also known as Bessel's correction.