Key Takeaways:
- Manually calculating loan payments in Excel with the
PMT()function is prone to errors due to complex syntax, mandatory rate/period adjustments, and confusing sign conventions. - Excelmatic simplifies this process entirely by allowing you to ask financial questions in natural language (e.g., “What's my monthly mortgage payment?”), delivering instant, accurate answers without formulas.
- The AI-powered tool excels at advanced tasks like generating full amortization schedules and conducting “what-if” analyses from a single prompt, translating complex manual work into simple conversations.
- For professionals who need reliable financial calculations without the technical hassle, adopting Excelmatic is the fastest path from financial questions to actionable insights.
Excel is a powerhouse for financial calculations, from simple budgeting to complex corporate finance models. One of the most fundamental tasks is calculating periodic payments for a loan or an investment. Traditionally, this required mastering Excel's PMT() function, a versatile tool for anyone dealing with mortgages, loans, or savings plans.
However, the landscape of data analysis is changing. While understanding the mechanics of financial functions is valuable, modern AI tools offer a faster, more intuitive path to the same answers.
This guide explores both methods. We'll walk through the traditional way of using the PMT() function and its related formulas. Then, we'll introduce a smarter alternative—using an AI agent like Excelmatic—to show you how you can get instant financial insights just by asking questions in plain language.
Two Ways to Get Your Answer
Let's say you want to calculate the monthly payment for a typical 30-year, $300,000 mortgage with a 4.5% annual interest rate.
The Traditional Formula Method
In a standard Excel sheet, you would use the PMT() function, carefully adjusting the rate and term for monthly payments. The formula would be:
=PMT(4.5%/12, 30*12, 300000)
This gives you a monthly payment of approximately $1,520.06.
The AI Agent Method (with Excelmatic)
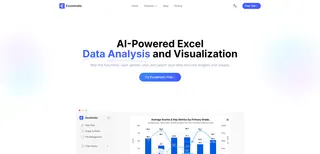
With an AI agent like Excelmatic, you simply upload your spreadsheet (or just have the data handy) and ask a direct question:
What is the monthly payment for a $300,000 mortgage over 30 years with a 4.5% annual interest rate?
Excelmatic instantly processes your request, performs the calculation, and gives you the answer without you ever touching a formula.
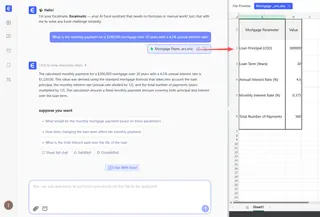
Now, let's dive deeper into the nuts and bolts of the traditional method before exploring more AI-powered shortcuts.
The Traditional Method: Understanding the PMT() Function
The PMT() function in Excel calculates the periodic payment required to settle a loan or investment with constant payments and a fixed interest rate.
PMT() Function Syntax and Parameters
The syntax of the PMT() function is:
=PMT(rate, nper, pv, [fv], [type])
Let's break down each parameter:
rate: The interest rate for each period. If your loan has a 4.5% annual interest rate but payments are monthly, you must use4.5%/12.nper: The total number of payment periods. For a 30-year loan with monthly payments, you'd use30*12or 360 periods.pv: The present value, or the total amount that a series of future payments is worth now. For a loan, this is the principal amount borrowed.fv(optional): The future value, or a cash balance you want to attain after the last payment is made. If omitted, it defaults to0(meaning the loan is fully paid off).type(optional): A number indicating when payments are due. Use0for payments at the end of the period (default) or1for payments at the beginning.
It's important to understand the cash flow convention in Excel: money you pay out (like a loan payment) is represented by a negative number, while money you receive (like the initial loan amount) is positive. This is why PMT() results are typically negative.
Understanding Payment Frequency Adjustments
A common source of errors is failing to align the rate and nper arguments with the payment frequency. Most loans have an annual interest rate, but payments are made monthly. You must adjust accordingly.
- Monthly:
annual rate / 12,number of years * 12 - Quarterly:
annual rate / 4,number of years * 4 - Semi-Annually:
annual rate / 2,number of years * 2
This table summarizes the adjustments for a 5-year loan with a 6% annual interest rate:
| Payment Frequency | Rate Adjustment | Period Adjustment | Adjusted Rate | Adjusted Periods |
|---|---|---|---|---|
| Monthly | Annual ÷ 12 | Years × 12 | 0.5% | 60 |
| Quarterly | Annual ÷ 4 | Years × 4 | 1.5% | 20 |
| Semi-Annually | Annual ÷ 2 | Years × 2 | 3% | 10 |
| Annually | No change | No change | 6% | 5 |
Getting these adjustments right is critical for an accurate calculation.
Common Uses: The Old Way vs. The New Way
Let's see how both methods handle the two most common financial calculations.
Calculating Mortgage Loan Payments
Let's walk through a real-life example:
- Loan amount: $400,000
- Interest rate: 6% annually
- Loan term: 20 years
- Payment frequency: Monthly
The Traditional Method: Using the PMT() Function
First, we need to adjust the rate and periods:
- Adjusted rate:
6%/12(0.5% per month) - Adjusted periods:
20*12(240 months)
The formula would be:
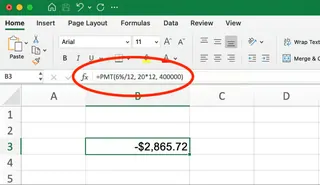
=PMT(6%/12, 20*12, 400000)
This gives a result of -$2,865.72. This is your monthly mortgage payment.
The AI Shortcut: Using Excelmatic
With Excelmatic, you skip the manual adjustments. You just ask:
Calculate the monthly payment on a $400,000 loan for 20 years with a 6% annual interest rate.
Excelmatic interprets your request, understands that "annual interest rate" and "monthly payment" require an adjustment, and delivers the correct answer of $2,865.72 instantly.
Calculating Savings and Investment Contributions
The PMT() function can also calculate how much you need to save regularly to reach a future financial goal.
Suppose you want to save $50,000 in 18 years with an estimated 6% annual return, contributing monthly.
The Traditional Method: Using the PMT() Function
In this case, the parameters change:
- Future value (fv):
50000(your goal) - Present value (pv):
0(you're starting from scratch) - Rate:
6%/12(0.5% monthly) - Periods:
18*12(216 months)
The formula would be:
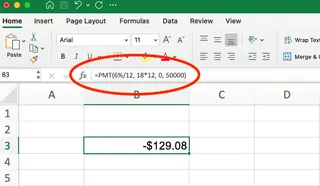
=PMT(6%/12, 18*12, 0, 50000)
This returns -$129.08, meaning you need to deposit about $130 monthly to reach your goal.
The AI Shortcut: Using Excelmatic
Again, you can use a simple, conversational prompt:
How much do I need to save each month to have $50,000 in 18 years, assuming a 6% annual return?
Excelmatic understands the goal and provides the required monthly contribution without you needing to remember which parameter is pv and which is fv.
Common Errors and How to Avoid Them
Working with the PMT() function can be tricky. Here are common pitfalls:
#NUM!or#VALUE!Errors: These often occur due to invalid inputs, like text in a number field or an interest rate so low the loan can never be paid off.- Forgetting Frequency Adjustments: The most common mistake is using an annual rate (e.g.,
6%) for monthly payments instead of the monthly rate (6%/12). - Incorrect Signs: Forgetting that outgoing payments are negative can lead to confusing results.
- Mixing up Periods: Ensuring
npermatches therateperiod (e.g., both are monthly) is crucial.
This is where an AI agent provides a significant advantage. By interpreting natural language, Excelmatic eliminates syntax errors, parameter mix-ups, and frequency adjustment mistakes, as it handles the technical translation behind the scenes.
Advanced Analysis: A Family of Functions vs. A Single AI
The PMT() function is just one member of Excel's financial function family. To get a full picture of a loan, you often need to use several others.
| Function | What It Does | Traditional Excel Formula | Excelmatic Prompt |
|---|---|---|---|
| IPMT() | Calculates the interest portion of a specific payment. | =IPMT(rate, per, nper, pv) |
"How much of my 12th payment is interest?" |
| PPMT() | Calculates the principal portion of a specific payment. | =PPMT(rate, per, nper, pv) |
"How much of my 12th payment goes to principal?" |
| NPER() | Calculates the number of periods to pay off a loan. | =NPER(rate, pmt, pv) |
"How long to pay off my loan if I pay $2000/month?" |
| RATE() | Calculates the interest rate of a loan. | =RATE(nper, pmt, pv)*12 |
"What's the interest rate on a 30-year, $300k loan with $1520 payments?" |
The AI Advantage: From Single Answers to Full Reports
While you can piece together an analysis using these individual functions, it's time-consuming. An AI agent can go much further, much faster. For instance, instead of calculating IPMT and PPMT for each period, you could simply ask Excelmatic:
Create a complete amortization schedule for my $400,000 loan.
Excelmatic can generate a full table showing the breakdown of principal and interest for every single payment over the life of the loan, a task that would take significant time to build manually in Excel.
Traditional Formulas vs. AI: A Quick Comparison
| Feature | Traditional PMT() Function |
Excelmatic (AI Agent) |
|---|---|---|
| Learning Curve | Steep: Requires memorizing syntax, parameters, and rules. | Minimal: Uses plain language. |
| Speed | Manual: Requires typing formulas and adjusting parameters. | Instant: Asks a question, gets an answer. |
| Error-Proneness | High: Prone to syntax errors, sign mistakes, and frequency errors. | Low: Interprets user intent, avoiding common formula mistakes. |
| Flexibility | Moderate: Requires combining multiple functions for deeper analysis. | High: Can answer follow-up questions and generate full reports or charts. |
| Advanced Analysis | Complex: Building an amortization schedule or scenario analysis is manual. | Simple: Can generate complex reports from a single prompt. |
Conclusion
Whether you're a financial analyst, a small business owner, or just planning your personal finances, understanding how to calculate loan and investment payments is essential. The traditional path of mastering Excel's PMT() function and its counterparts provides a solid, foundational understanding.
However, the future of data analysis is about efficiency and accessibility. AI-powered tools like Excelmatic are not just a shortcut; they are a smarter way to work. They empower you to focus on the financial questions you want to answer, not on the complex syntax needed to ask them. By handling the calculations, adjustments, and even generating comprehensive reports, these tools let you move from data to decision in record time.
Ready to streamline your financial analysis and get instant payment calculations? Try Excelmatic today and discover how easy it is to make smarter financial decisions with AI.
FAQ
What is the PMT() function in Excel?
ThePMT() function in Excel calculates the payment for a loan based on constant payments and a constant interest rate. It's commonly used for mortgages, auto loans, and investment calculations.
When should I use the PMT function instead of an AI tool?
Using the PMT() function manually is great for learning the mechanics of financial calculations or for building highly customized, auditable financial models where every step must be visible in a formula. For quick answers, reporting, and avoiding manual errors, an AI tool like Excelmatic is often more efficient.
Why does my PMT() function return a negative number?
ThePMT() function follows Excel's cash flow convention where outgoing payments appear as negative numbers. If you want to display the payment as a positive number, simply add a negative sign before your PMT formula (e.g., =-PMT(...)). AI tools like Excelmatic often present this more intuitively, directly stating the payment amount.
What's the difference between PMT, IPMT, and PPMT() functions?
PMT() calculates the total payment amount, IPMT() calculates only the interest portion of a specific payment, and PPMT() calculates only the principal portion. For any given period, IPMT + PPMT will always equal PMT.
How do I account for an initial down payment in my calculation?
With the PMT() function, you subtract the down payment from the total price before entering it as the present value (pv). For example, for a $350,000 house with a $50,000 down payment, your pv is $300,000. With an AI tool like Excelmatic, you can often state this directly, such as "calculate payments for a $350,000 house with a $50,000 down payment," and it will handle the math for you.






