Key Takeaways
- Understanding variable relationships is crucial for business decisions, but traditional Excel methods require technical formula knowledge that many business users lack
- Excelmatic's AI approach eliminates the need for statistical expertise - simply describe what you want to analyze in plain language and get instant correlation insights
- The platform automatically handles data validation and error checking, avoiding common formula mistakes that can lead to incorrect business conclusions
- For non-technical professionals in marketing, sales, and operations, Excelmatic provides the fastest path from raw data to actionable relationship insights
Analyzing the relationship between two sets of data is a fundamental task in data analysis. By calculating the correlation coefficient, you can quickly assess whether two variables move together, move in opposite directions, or have no relationship at all. This is crucial in fields like finance, where you might analyze stock returns against interest rates, or in marketing, to see how ad spend affects revenue.
In this guide, we'll explore two powerful methods for analyzing correlation in Excel: the traditional formula-based approach and a modern, AI-powered solution. You'll learn how to apply both and see how AI tools are making complex analysis more accessible than ever.
Understanding Correlation
Before diving in, let's clarify what we're measuring. Correlation analysis measures the strength and direction of the linear relationship between two variables. The result, known as the correlation coefficient (or Pearson correlation coefficient), ranges from -1 to 1:
- 1 indicates a perfect positive correlation (as one variable increases, the other increases).
- -1 indicates a perfect negative correlation (as one variable increases, the other decreases).
- 0 indicates no linear correlation.
For instance, you might find a strong positive correlation (close to 1) between advertising spend and sales, or a strong negative one (close to -1) between interest rates and bond prices.
Method 1: The Traditional Approach with the CORREL() Function
Excel's CORREL() function is a powerful statistical tool for calculating the correlation coefficient directly. It's reliable and has been a go-to for analysts for years.
CORREL() Syntax and Arguments
To use the CORREL() function, you need to understand its simple syntax:
=CORREL(array1, array2)
array1: The first range of values.array2: The second range of values.
A critical requirement is that both arrays must have the same number of data points. If they don't, CORREL() will return a #N/A error.
How to Use CORREL() in Excel
Follow these steps to calculate correlation using the CORREL() function:
- Enter your two data sets in separate columns.
- Click on the cell where you want the correlation coefficient to appear.
- Type the
CORREL()formula, referencing your data ranges. - Press Enter to display the result.
For example, if your data for interest rates and bond prices is in columns A and B from rows 2 to 11:
=CORREL(A2:A11, B2:B11)
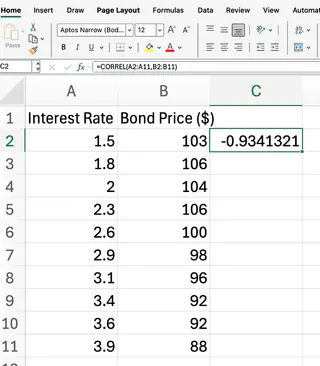
Our formula returns the correlation coefficient between the two data sets. Based on financial theory, we expect a result close to -1, indicating a strong negative correlation—as interest rates rise, bond prices typically fall.
Method 2: The AI-Powered Approach with Excelmatic
While the CORREL() function is effective, what if you could get the same result without memorizing formulas? This is where Excelmatic shines. Excelmatic allows you to perform complex data analysis by simply asking questions in plain language.
How to Analyze Correlation with Excelmatic
Instead of typing formulas, you can get instant answers, charts, and AI insights. Here’s how you'd solve the same problem with Excelmatic:
- Upload your file containing the two data sets (e.g., interest rates and bond prices).
- Ask a simple question in the chat interface. For example:
- "What is the correlation between the 'Interest Rate' and 'Bond Price' columns?"
- Or more broadly: "Analyze the relationship between interest rates and bond prices."
- Get instant results. Excelmatic will process your request and provide the correlation coefficient instantly.
What makes this approach powerful is that Excelmatic often goes beyond just giving you a number. It can also generate a scatter plot to visualize the relationship and provide a brief, AI-driven interpretation of the result, saving you even more time.
Comparing the Methods: CORREL() vs. Excelmatic
| Feature | CORREL() Function (Traditional) |
Excelmatic (AI-Powered) |
|---|---|---|
| Ease of Use | Requires knowledge of function syntax and cell references. | Uses simple, plain English commands. No formulas to remember. |
| Speed | Fast for experienced users. | Instantaneous. Eliminates time spent recalling and typing formulas. |
| Error Handling | Returns cryptic errors like #N/A or #DIV/0!. |
Provides user-friendly feedback if data is inconsistent or missing. |
| Insights | Provides a single numerical output (the coefficient). | Delivers the coefficient, plus potential visualizations and AI-generated interpretations. |
| Learning Curve | Moderate; requires learning specific Excel functions. | Minimal; if you can ask a question, you can use it. |
Interpreting the Results
Whether you use CORREL() or Excelmatic, interpreting the resulting coefficient is key. The value will always fall between -1 and 1:
- Values close to 1: Strong positive correlation (as one variable increases, so does the other).
- Values close to -1: Strong negative correlation (as one variable increases, the other decreases).
- Values close to 0: Little or no linear relationship.
Remember a crucial point: correlation does not imply causation. A high correlation coefficient simply indicates that a relationship exists, not that one variable causes the other to change.
Common Errors with the Manual Method
When using the CORREL() function, you may encounter some common errors. Understanding these can help you troubleshoot quickly.
#N/Aerror: Occurs if the two arrays have different numbers of data points.#DIV/0!error: Happens if either array has less than two data points or if the standard deviation of either array is zero.#VALUE!error: Appears if non-numeric values are included in the data ranges.
Ensuring your data ranges are equal in length and contain only numeric values will help you avoid these issues. One of the benefits of Excelmatic is that it handles these data validation checks for you, often providing clearer guidance on how to fix the source data.
Conclusion
The CORREL() function remains an essential tool in any Excel analyst's toolkit for its direct and reliable calculations. However, the landscape of data analysis is evolving. Excelmatic is democratizing data analysis, making it faster, more intuitive, and more insightful for business users.
By allowing you to use natural language to ask complex questions, Excelmatic empowers marketing, sales, and operations professionals to move beyond manual formulas and focus on what truly matters: understanding the story their data is telling and making better business decisions.
Ready to uncover hidden relationships in your data without the technical complexity? Try Excelmatic today and experience the power of AI-driven correlation analysis for yourself.
Whether you stick with the classics or embrace the AI revolution, mastering correlation analysis is a valuable skill for anyone working with data.






